Angle polaire , mesure principal ( exo débuté )
17 messages
- Page 1 sur 1
Angle polaire , mesure principal ( exo débuté )
Bonjour !!
Alors voilà jai un exo à faire et jaurais voulu de votre aide , je lai déjà bien débuté mais il y a des endroits où je bloque :
Trouver la mesure principale de H ( 3 ; 17pi / 4) : jai trouvé pi/4
I ( racine de 2 ; 5pi/4) : jai trouvé -3pi/4
J ( ¾ ; 20pi) LA JE VOIT PAS COMMENT ON FAIT POUR 20pi
K ( 2 ; -5pi/3) : jai trouvé pi/3
L ( 4 ; -7pi/6) : jai trouvé 5pi/6
M ( ¼ ; 37pi /4) : jai trouvé -3pi/4
N ( 3 ; -1789 pi) JE BLOQUE AUSSI
P ( 2; 26pi/3) JE BLOQUE
Merci à ceux qui vont me répondre et vérifier par ailleur que mes réponses sont justes
@+
Alors voilà jai un exo à faire et jaurais voulu de votre aide , je lai déjà bien débuté mais il y a des endroits où je bloque :
Trouver la mesure principale de H ( 3 ; 17pi / 4) : jai trouvé pi/4
I ( racine de 2 ; 5pi/4) : jai trouvé -3pi/4
J ( ¾ ; 20pi) LA JE VOIT PAS COMMENT ON FAIT POUR 20pi
K ( 2 ; -5pi/3) : jai trouvé pi/3
L ( 4 ; -7pi/6) : jai trouvé 5pi/6
M ( ¼ ; 37pi /4) : jai trouvé -3pi/4
N ( 3 ; -1789 pi) JE BLOQUE AUSSI
P ( 2; 26pi/3) JE BLOQUE
Merci à ceux qui vont me répondre et vérifier par ailleur que mes réponses sont justes
@+
up :hum: merci :happy2:
:ptdr: désolé pour le :hum: je rassure je n'était pas dans cet état là :lol4:
:chaise: je pense que les modérateurs doivent en avoir marre à force comme les gens qui ne lisent pas les règles du forum et , je comprend que mon up vous ait " irrité" , pardon :triste: sincérement
:ptdr: désolé pour le :hum: je rassure je n'était pas dans cet état là :lol4:
:chaise: je pense que les modérateurs doivent en avoir marre à force comme les gens qui ne lisent pas les règles du forum et , je comprend que mon up vous ait " irrité" , pardon :triste: sincérement
La méthode générale est fondée sur la définition pure et dure de la mesure principale.
Soit D la mesure donnée, M la mesure principale ; il faut trouver n entier tel que :
 \le \pi)
Et alors on aura)
 \le \pi)
Je retranche D aux trois membres :
 \le \pi-D)
Ce qui se ramène aux deux inégalités :
 \ \ \ [1])
 \le \pi-D \ \ \ [2])
J'ajoute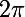 aux deux membres de [1] :
aux deux membres de [1] :
+(2\pi) \ \ \ [1'])
\times (2\pi) \ \ \ [1'])
Je regroupe les deux inégalités :
 \le \pi-D < (n+1)\times (2\pi))
Et enfin, je divise par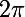 :
:
)
Cette expression montre clairement que n est la partie entière de
 avec E[x] = partie entière de x !
avec E[x] = partie entière de x !
Exemple sur les cas où tu bloques :



D'où :
=\frac{26\pi}{3}-4\times (2\pi))
=\pi \times \frac{26}{3}-4\times (2)=\pi \times \frac{2}{3})


D'où :
=-1789\pi+895\times (2\pi)=\pi)
Quant à , c'est évident puisque 20=2*10 ! La mesure principale est 0 ! Mais ma formule marche aussi, bien sûr :ptdr:
, c'est évident puisque 20=2*10 ! La mesure principale est 0 ! Mais ma formule marche aussi, bien sûr :ptdr:
Soit D la mesure donnée, M la mesure principale ; il faut trouver n entier tel que :
Et alors on aura
Je retranche D aux trois membres :
Ce qui se ramène aux deux inégalités :
J'ajoute
Je regroupe les deux inégalités :
Et enfin, je divise par
Cette expression montre clairement que n est la partie entière de
Exemple sur les cas où tu bloques :
D'où :
D'où :
Quant à
ça allère :ptdr:
Tu allères de gallérer avec la langue de Mollères...
Bon, trêves de plaisanteries, oui, Quidam, tu as raison, j'ai eu un doute mais je ne me souvenais plus si c'était -pi ou +pi qui était exclu.
Et sinon, pour @louette, Quidam fait en gros la même chose que ce que tu as fait pour 37pi/4, sauf qu'il donne une formule générale.
Tu allères de gallérer avec la langue de Mollères...
Bon, trêves de plaisanteries, oui, Quidam, tu as raison, j'ai eu un doute mais je ne me souvenais plus si c'était -pi ou +pi qui était exclu.
Et sinon, pour @louette, Quidam fait en gros la même chose que ce que tu as fait pour 37pi/4, sauf qu'il donne une formule générale.
J'ai une dernière question :we:
En fait on me demande de déterminez leurs coordonnées cartésiennes , dans le cours on a mis des coordonnées cartésiennes en coordonnées polaires mais pas l'inverse , c'est possible de savoir comment on fait avec l'un de mes points ?
Merci MOoOodératEeeEuRRr and QUUUUiiiiiDaAaAM ( oula ça vas pas mieux moi aujourdh'ui :zen: )
En fait on me demande de déterminez leurs coordonnées cartésiennes , dans le cours on a mis des coordonnées cartésiennes en coordonnées polaires mais pas l'inverse , c'est possible de savoir comment on fait avec l'un de mes points ?
Merci MOoOodératEeeEuRRr and QUUUUiiiiiDaAaAM ( oula ça vas pas mieux moi aujourdh'ui :zen: )
@lOuEttE c'est marrant , j'ai casi les même exo que toi ?! :doh:
Bref , moi j'en profite pour dire que j'ai la même question et j'aimerai bien quand m'éclaire sur ce point ( coordonnées cartésiennes) car je ne comprend pas très bien !
Désolé @lOuEttE si j'ai " grugé " dans la conversation :++: tu me dis si tu ne veux pas que mon message soit ici au pire je crée un autre topic mais ceci ne servirait à rien
Bref , moi j'en profite pour dire que j'ai la même question et j'aimerai bien quand m'éclaire sur ce point ( coordonnées cartésiennes) car je ne comprend pas très bien !
Désolé @lOuEttE si j'ai " grugé " dans la conversation :++: tu me dis si tu ne veux pas que mon message soit ici au pire je crée un autre topic mais ceci ne servirait à rien
coordonnées cartésiennes
:ptdr: alpha :ptdr: merci ^^
bon sinon ABC100 c'est pas bien grave :zen: mais c'est bizarre qu'on ai les même exo :doh: bref !
si quelqu'un pourrait m'aider pour les coordonnées cartésiennes
MERCI !!!
bon sinon ABC100 c'est pas bien grave :zen: mais c'est bizarre qu'on ai les même exo :doh: bref !
si quelqu'un pourrait m'aider pour les coordonnées cartésiennes
MERCI !!!
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
