Angle au centre
24 messages
- Page 1 sur 2 - 1, 2
angle au centre
Bonjour,
Je vous expose mon problème.
Je suis métreur sur apibatiment et le souci est que je ne dispose pas de toutes les fonctions arithmétique. Les seules à ma disposition sont :
+ - * / ^ % rac(...) sin(...) cos(...) tan(...)
Je cherche à calculer la longueur d'un arc de cercle connaissant la corde et la flèche.
Je ne dispose pas de fonction tan-1
Donc je ne vois pas comment trouver l'angle au centre nommé a ? :mur:
Voilà où j'en suis.
' entrez vos valeur si dessous
flèche = 1088.9
corde = 6229.9
' debut du script
pi = 3.14159265358979323846264338327950288419716939937510
rayon = (flèche^2+(corde/2)^2)/(2×flèche)
invtan = corde / (2×(rayon-flèche))
a = ?
a × rayon × pi / 180
Je vous expose mon problème.
Je suis métreur sur apibatiment et le souci est que je ne dispose pas de toutes les fonctions arithmétique. Les seules à ma disposition sont :
+ - * / ^ % rac(...) sin(...) cos(...) tan(...)
Je cherche à calculer la longueur d'un arc de cercle connaissant la corde et la flèche.
Je ne dispose pas de fonction tan-1
Donc je ne vois pas comment trouver l'angle au centre nommé a ? :mur:
Voilà où j'en suis.
' entrez vos valeur si dessous
flèche = 1088.9
corde = 6229.9
' debut du script
pi = 3.14159265358979323846264338327950288419716939937510
rayon = (flèche^2+(corde/2)^2)/(2×flèche)
invtan = corde / (2×(rayon-flèche))
a = ?
a × rayon × pi / 180
bonjour,
d'apres Wikipedia on a (sauf erreur)
r = (c^2+4f^2)/(8f)
d'autre part la longueur de l'arc est proportionnelle a l'angle en radians ....
mais les calculs geometriques dans les triangles conduisent a definir l'angle par une ligne trigonometrique
il faut donc a un moment ou a un autre passer de la ligne trigonometrique a l'angle ......
d'apres Wikipedia on a (sauf erreur)
r = (c^2+4f^2)/(8f)
d'autre part la longueur de l'arc est proportionnelle a l'angle en radians ....
mais les calculs geometriques dans les triangles conduisent a definir l'angle par une ligne trigonometrique
il faut donc a un moment ou a un autre passer de la ligne trigonometrique a l'angle ......
Ça me donne le rayon :mur:
Mais ça ne résolve pas mon problème
Comment je trouve l'angle sans sin-1 cos-1 tan-1 ?
Merci quand même
Mais ça ne résolve pas mon problème
Comment je trouve l'angle sans sin-1 cos-1 tan-1 ?
Merci quand même
siger a écrit:bonjour,
d'apres Wikipedia on a (sauf erreur)
r = (c^2+4f^2)/(8f)
d'autre part la longueur de l'arc est proportionnelle a l'angle en radians ....
mais les calculs geometriques dans les triangles conduisent a definir l'angle par une ligne trigonometrique
il faut donc a un moment ou a un autre passer de la ligne trigonometrique a l'angle ......
bonjour,
concernant le rayon:
^2+(r-f)^2=r^2)
ce qui donne

maintenant, il s'agit d'écrire une routine inversant la tangente. regarde ici
remarque: l'algorithme proposé par JJ est d'un excellent niveau mathématique, rapide mais incompréhensible au profane. 1ère solution: le recopier tel quel.
sinon, l'algorithme , basé sur la méthode de Newton est d'un niveau moindre, ce qui te posera moins de problème de maintenance (par exemple de trouver un ingénieur pour déboguer)
concernant le rayon:
ce qui donne
maintenant, il s'agit d'écrire une routine inversant la tangente. regarde ici
remarque: l'algorithme proposé par JJ est d'un excellent niveau mathématique, rapide mais incompréhensible au profane. 1ère solution: le recopier tel quel.
sinon, l'algorithme , basé sur la méthode de Newton est d'un niveau moindre, ce qui te posera moins de problème de maintenance (par exemple de trouver un ingénieur pour déboguer)
Méthode de Newton
la méthode de Newton, de résolution des équations, n'est pas trop difficile à comprendre , et nécessite d'écrire une équation de droite tangente. Elle conduit à la formule itérative:
}{f'(x_n)})
pour résoudre l'équation=0)
La suite de terme général) donne des valeurs approchées
donne des valeurs approchées
de la solution , démarre avec une valeur initiale et converge
et converge
si la valeur initiale est voisine de la solution.
ici, on veut inverser la tangente, donc résoudre l'équation d'inconnue et de donnée
et de donnée 
-u=0)
'(x)=1+tan^2(x))
-u}{1+tan^2(x_n)})
on revient au cosinus et sinus
sin(x_n)-u cos^2(x_n)})
on passe à l'arc double
-u (1+cos(2x_n)))
voilà donc l'algo de base
X=u (u est la valeur de la tangente filée en paramètre)
k=0
TANT QUE k<10
Y=2*X
X=X-0.5 (sin(Y)-u(1+cos(Y)))
k=k+1
FIN TANT QUE
PRINT "arctan(u)", X
ici, la valeur de tangente est donnée par
si est grande ,
est grande , 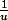 est petite,
est petite,
on change alors u en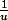 ,
,
l'algo calcule la solution de l'équation d'inconnue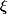
=\frac{1}{u})
et à la fin vaut
vaut 
la méthode de Newton, de résolution des équations, n'est pas trop difficile à comprendre , et nécessite d'écrire une équation de droite tangente. Elle conduit à la formule itérative:
pour résoudre l'équation
La suite de terme général
de la solution , démarre avec une valeur initiale
si la valeur initiale est voisine de la solution.
ici, on veut inverser la tangente, donc résoudre l'équation d'inconnue
on revient au cosinus et sinus
on passe à l'arc double
voilà donc l'algo de base
X=u (u est la valeur de la tangente filée en paramètre)
k=0
TANT QUE k<10
Y=2*X
X=X-0.5 (sin(Y)-u(1+cos(Y)))
k=k+1
FIN TANT QUE
PRINT "arctan(u)", X
ici, la valeur de tangente est donnée par
si
on change alors u en
l'algo calcule la solution de l'équation d'inconnue
et à la fin
:hein: Je crois que mes limites sont atteintes :doh:
Je n'ai qu'un niveau 2nd :stupid_in
De plus je ne suis pas sur que ce soit possible dans le logiciel il n'est pas possible de faire de boucles.
J'avoue que je suis largué
merci quand même
Je n'ai qu'un niveau 2nd :stupid_in
De plus je ne suis pas sur que ce soit possible dans le logiciel il n'est pas possible de faire de boucles.
J'avoue que je suis largué
merci quand même
busard_des_roseaux a écrit:Méthode de Newton
la méthode de Newton, de résolution des équations, n'est pas trop difficile à comprendre , et nécessite d'écrire une équation de droite tangente. Elle conduit à la formule itérative:
pour résoudre l'équation
La suite de terme généraldonne des valeurs approchées
de la solution , démarre avec une valeur initialeet converge
si la valeur initiale est voisine de la solution.
ici, on veut inverser la tangente, donc résoudre l'équation d'inconnueet de donnée
on revient au cosinus et sinus
on passe à l'arc double
voilà donc l'algo de base
X=u (u est la valeur de la tangente filée en paramètre)
k=0
TANT QUE k<10
Y=2*X
X=X-0.5 (sin(Y)-u(1+cos(Y)))
k=k+1
FIN TANT QUE
PRINT "arctan(u)", X
ici, la valeur de tangente est donnée par
siest grande ,
est petite,
on change alors u en,
l'algo calcule la solution de l'équation d'inconnue
et à la finvaut
Je suis largué
Je remets les variables avec les valeurs trouvés
flèche = 1088.9
corde = 6229.9
' debut du script
pi = 3.142
f = flèche
c = corde
r = (c^2 + 4 × f^2)/(8 × f) = 4999.824 <--- donnée fausse dû à la limitation du logiciel, normalement 5000
invtan = c/ (2×(r-f)) = 0.796
a = :hum:
a × r × pi / 180
Maintenant, si je fais sur une calculatrice tan-1(0.796) ca me donne bien l'angle a
Du coup je ne sais plus :mur:
Je remets les variables avec les valeurs trouvés
flèche = 1088.9
corde = 6229.9
' debut du script
pi = 3.142
f = flèche
c = corde
r = (c^2 + 4 × f^2)/(8 × f) = 4999.824 <--- donnée fausse dû à la limitation du logiciel, normalement 5000
invtan = c/ (2×(r-f)) = 0.796
a = :hum:
a × r × pi / 180
Maintenant, si je fais sur une calculatrice tan-1(0.796) ca me donne bien l'angle a
Du coup je ne sais plus :mur:
busard_des_roseaux a écrit:le souci c'est que tout les algorithmes contiennent des boucles.
je te propose une solution approchée
évidemment, la somme est infinie, on coupe à un moment et on dit que le reste est négligeable
Re
- comme je l'ai deja indiqué les calculs a partir de la fleche et de la corde conduisent a la determination d'une ligne trigonometrique
-le calcul de la longueur de l'arc se fait a partir de la valeur de l'angle en radians
DONC il faut a un moment ou a un autre passer de la ligne a l'angle
(sauf sil'angle est petit, ce qui n'est pas le cas dans ton exemple)
soit en utilisant une fonction inverse arcsin, arctan, ....(ou une approximation par un polynome) que ce soit "a la main " ou avec un algorithme
soit en recherchant la valeur de l'angle dans une table
Je dois dire qu'apres avoir vu ta piece jointe, je comprends mal ton probleme!
en effet tu indiques l'angle au centre sur ton dessin: comment l'as tu determiné? j'avais cru comprendre que c'est justement ce que tu cherches a calculer!
- comme je l'ai deja indiqué les calculs a partir de la fleche et de la corde conduisent a la determination d'une ligne trigonometrique
-le calcul de la longueur de l'arc se fait a partir de la valeur de l'angle en radians
DONC il faut a un moment ou a un autre passer de la ligne a l'angle
(sauf sil'angle est petit, ce qui n'est pas le cas dans ton exemple)
soit en utilisant une fonction inverse arcsin, arctan, ....(ou une approximation par un polynome) que ce soit "a la main " ou avec un algorithme
soit en recherchant la valeur de l'angle dans une table
Je dois dire qu'apres avoir vu ta piece jointe, je comprends mal ton probleme!
en effet tu indiques l'angle au centre sur ton dessin: comment l'as tu determiné? j'avais cru comprendre que c'est justement ce que tu cherches a calculer!
Oui c'est bien l'angle que je cherche
j'ai fais le dessin pour mieux expliquer mon problème et pour me permettre de m'auto contrôler
j'ai fais le dessin pour mieux expliquer mon problème et pour me permettre de m'auto contrôler
siger a écrit:Re
- comme je l'ai deja indiqué les calculs a partir de la fleche et de la corde conduisent a la determination d'une ligne trigonometrique
-le calcul de la longueur de l'arc se fait a partir de la valeur de l'angle en radians
DONC il faut a un moment ou a un autre passer de la ligne a l'angle
(sauf sil'angle est petit, ce qui n'est pas le cas dans ton exemple)
soit en utilisant une fonction inverse arcsin, arctan, ....(ou une approximation par un polynome) que ce soit "a la main " ou avec un algorithme
soit en recherchant la valeur de l'angle dans une table
Je dois dire qu'apres avoir vu ta piece jointe, je comprends mal ton probleme!
en effet tu indiques l'angle au centre sur ton dessin: comment l'as tu determiné? j'avais cru comprendre que c'est justement ce que tu cherches a calculer!
Urgence Les Amis
voila alors je n'arrive pas a resoudre ce dns de math aidez moi plizzz vous me sauvez la vie et desole dintervenir dans la conversation mais je ne trouve pas comment creer ma propre discussion
Le maire de Levillage, Mr Dupont, souhaite fleurir une parcelle de terrain triangulaire ABC tels que AB = 6 dam et BC = 12 dam. Il souhaite que la partie fleurie BMFP soit rectangulaire. (Rappel : 1dam = 1décamètre = 10m)
Soit un point M sur le segment [AB] tel que AM = x dam. La parallèle à (BC) passant par M coupe le segment [AC] en F et la parallèle à (AB) passant par F coupe le segment [BC] en P. (soit le rectangle BMFP)
On note f(x) , laire, en dam², de la partie fleurie BMFP en fonction de x.
Quel est lensemble de définition de f ?
Déterminer la valeur exacte de AC.
Montrer que PC=12-2x puis calculer BP en fonction de x.
Exprimer f(x) .
Montrer que f(x)=18-2(x-3)²
Déterminer une valeur approchée en dam² (à lunité près) de laire de la partie fleurie si AM = V7 dam.
Déterminer, par le calcul, la ou les longueurs de AM pour que laire de la partie fleurie soit égale à 18 dam².
a. Tracer la courbe représentative de la fonction f dans un repère orthogonal (2cm pour une unité en abs, 1cm pour 2 unités en ord).
b. Conjecturer, à laide de ce graphique, lexistence du maximum.
c. Montrer que f(x)-f(3)=-2(x-3)² puis montrer la conjecture émise.
Le maire de Levillage, Mr Dupont, souhaite fleurir une parcelle de terrain triangulaire ABC tels que AB = 6 dam et BC = 12 dam. Il souhaite que la partie fleurie BMFP soit rectangulaire. (Rappel : 1dam = 1décamètre = 10m)
Soit un point M sur le segment [AB] tel que AM = x dam. La parallèle à (BC) passant par M coupe le segment [AC] en F et la parallèle à (AB) passant par F coupe le segment [BC] en P. (soit le rectangle BMFP)
On note f(x) , laire, en dam², de la partie fleurie BMFP en fonction de x.
Quel est lensemble de définition de f ?
Déterminer la valeur exacte de AC.
Montrer que PC=12-2x puis calculer BP en fonction de x.
Exprimer f(x) .
Montrer que f(x)=18-2(x-3)²
Déterminer une valeur approchée en dam² (à lunité près) de laire de la partie fleurie si AM = V7 dam.
Déterminer, par le calcul, la ou les longueurs de AM pour que laire de la partie fleurie soit égale à 18 dam².
a. Tracer la courbe représentative de la fonction f dans un repère orthogonal (2cm pour une unité en abs, 1cm pour 2 unités en ord).
b. Conjecturer, à laide de ce graphique, lexistence du maximum.
c. Montrer que f(x)-f(3)=-2(x-3)² puis montrer la conjecture émise.
sonata a écrit:Avec précision est un bien grand motles arrondis sont pas toujours bon mais globalement c'est pas mal
On en reviens donc au probleme de base:
tu veux determiner la valeur d'un angle en radian connaissant la valeur d'une de se lignes trigonometriques
on a par exemple
tan(A) = (1/2)*(c/(r-f)) = x avec r = ....
d'autre part on a une approximation de la foncrion inverse arc tan(x)
A =arc tan (x) = x -x^3/3 + x^5/3 -x^7/7+....= x*(1 - x^2/2 + x^4/4 - x^6/6 + ..)
un algorithme simple pourrait etre (sauf erreur):
initialiser f, c , n
calculer r, puis x
A = 1
a=1
pour i de 1 à n
a=-a
A= A+a*(x)^2î/(2i)
fin i
A = A*x
imprimer A
sonata a écrit:Avec précision est un bien grand motles arrondis sont pas toujours bon mais globalement c'est pas mal
Donc on en revient au probleme:
determiner un angle A en radians connaissant un ligne trigonometrique de cet angle A
On a tan(A) =(2tan(A/2))/(1-tan(A/2)²) = X , avec tan(A/2) = (c/2)/(r-f)
X = (4c*(r-f))/(4(r-f)²-c²) et r -f = (c²-4f²)/8f
par suite A = arctan (X) = (X - X^3/3 + X^5/5 - X^7/7+... )
Un algorithme simple pourrait etre
initialiser f, c , n
calculer r, X
a=1
A = X
pour j = 1 à n
a=-a
k = 2j + 1
A = A + a*(X)^k /k
fin j
imprimer A
24 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

