Analyse combinatoire
19 messages
- Page 1 sur 1
Analyse combinatoire
Bonjour, un petit problème avec un exercice.
Le code d'un coffre est constitué de 5 chiffres.
1) combien y a-t-il de codes possibles.
2) combien y a-t-il de codes avec 3 chiffres paires et deux chiffres 9?
1) combien y a-t-il de codes avec au moins un chiffre 0?
1) je pense que :
AIn = 105 = 100 000
==> 10 x 10 x 10 x 10 x 10.
2) Il faut en prendre 3 parmi 5 (0, 2 , 4 , 6 ,8) avec répétition donc un arrangement avec répétition.
==>Anp = 5^3 = 125 possibilités pour les 3 premiers.
Après je bloque. comment tenir compte des deux 9 sachant qu'ils ne sont pas forcément à la fin?
3)Je bloque également.
Merci de votre aide.
Le code d'un coffre est constitué de 5 chiffres.
1) combien y a-t-il de codes possibles.
2) combien y a-t-il de codes avec 3 chiffres paires et deux chiffres 9?
1) combien y a-t-il de codes avec au moins un chiffre 0?
1) je pense que :
AIn = 105 = 100 000
==> 10 x 10 x 10 x 10 x 10.
2) Il faut en prendre 3 parmi 5 (0, 2 , 4 , 6 ,8) avec répétition donc un arrangement avec répétition.
==>Anp = 5^3 = 125 possibilités pour les 3 premiers.
Après je bloque. comment tenir compte des deux 9 sachant qu'ils ne sont pas forcément à la fin?
3)Je bloque également.
Merci de votre aide.
Salut !
J'ai pas compris tes réponses...
1°) Un chiffre est un élément de l'ensemble à éléments
éléments  . Donc si le code comporte cinq chiffre, l'ensemble des codes possibles est l'ensemble
. Donc si le code comporte cinq chiffre, l'ensemble des codes possibles est l'ensemble  . Donc tu en déduis bien qu'il y a
. Donc tu en déduis bien qu'il y a 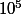 combinaisons possibles.
combinaisons possibles.
2°) Dans , l'ensemble
, l'ensemble  des chiffres pairs est composé de
des chiffres pairs est composé de  éléments
éléments  .
.
Ainsi, se donner un code avec chiffres pairs revient à se donner un sous-ensemble de
chiffres pairs revient à se donner un sous-ensemble de  .
.
J'ai pas compris tes réponses...
1°) Un chiffre est un élément de l'ensemble à
2°) Dans
Ainsi, se donner un code avec
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:Salut !
J'ai pas compris tes réponses...
1°) Un chiffre est un élément de l'ensemble àéléments
. Donc si le code comporte cinq chiffre, l'ensemble des codes possibles est l'ensemble
. Donc tu en déduis bien qu'il y a
combinaisons possibles.
2°) Dans, l'ensemble
des chiffres pairs est composé de
éléments
.
Ainsi, se donner un code avecchiffres pairs revient à se donner un sous-ensemble de
.
oui jusque là j'ai compris (on utilise pas la même notation, mais on a les mêmes réponses).
Seulement, dans le 2, on a bien 125 possibilités si la combinaison se termine par 99. Mais si les "9" peuvent se trouver n'importe où, comment dois-je calculer?
Ex : 9 4 2 6 9.
il faut d'abord choisir les 2 places où se trouveront les"9", soit C(5,2) (coefficient binomial), puis les 3 chiffres pairs (5x4x3), ce qui donne 10x5x4x3=600.
les nombres ne comportant pas de "0", sont au nombre de 9x9x9x9x9=59049, donc ceux comportant un "0" sont au nombre de 10^5=100000-59049=40951.
Dans ce raisonnement, on considère que 945=00945!
les nombres ne comportant pas de "0", sont au nombre de 9x9x9x9x9=59049, donc ceux comportant un "0" sont au nombre de 10^5=100000-59049=40951.
Dans ce raisonnement, on considère que 945=00945!
paquito a écrit:il faut d'abord choisir les 2 places où se trouveront les"9", soit C(5,2) (coefficient binomial), puis les 3 chiffres pairs (5x4x3), ce qui donne 10x5x4x3=600.
les nombres ne comportant pas de "0", sont au nombre de 9x9x9x9x9=59049, donc ceux comportant un "0" sont au nombre de 10^5=100000-59049=40951.
Dans ce raisonnement, on considère que 945=00945!
Mais en quoi C(2,5) s'occupe du placement des "9"? ça suppose de prends les duos sur 5 éléments, hors les "9" 'n'ont rien avoir avec les 5 chiffres paires.
nico253 a écrit:Mais en quoi C(2,5) s'occupe du placement des "9"? ça suppose de prends les duos sur 5 éléments, hors les "9" 'n'ont rien avoir avec les 5 chiffres paires.
Soit
Se donner deux chiffres égaux à 9 revient à choisir un sous-ensemble de
Attention,
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:Soitle code composé de cinq chiffres.
Se donner deux chiffres égaux à 9 revient à choisir un sous-ensemble deconstitué de deux éléments (ce sont ceux qui seront égaux à 9) : il y en a
.
Attention,n'est pas tout à fait un ensemble au sens mathématique du terme.
En gros, on choisit 2 sièges sur 5 pour les 9 et après on y incruste les 125 possibilités à chaque fois?
Seulement, l'énoncé ne précise pas que les nombres doivent être différents, donc au lieu de 5x4x3, on doit faire 5 x 5 x 5 = 125 non? (x10 en tout)
nico253 a écrit:En gros, on choisit 2 sièges sur 5 pour les 9 et après on y incruste les 125 possibilités à chaque fois?
Seulement, l'énoncé ne précise pas que les nombres doivent être différents, donc au lieu de 5x4x3, on doit faire 5 x 5 x 5 = 125 non? (x10 en tout)
Pourquoi x10 ?
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
nico253 a écrit:avec 125 à chaque ligne
9 9 . . .
9 . 9 . .
9 . . 9 .
9 . . . 9
. 9 9 . .
. 9 . 9 .
. 9 . . 9
. . 9 9 .
. . 9 . 9
. . . 9 9
C(2,5) = 5!/(2!*3!) placer les "9" et après les 125 solutions à chaque fois non?
Ah oui, je suis d'accord. J'avais pas calculé le
Oui, je suis d'accord avec toi : il y a
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:Ah oui, je suis d'accord. J'avais pas calculé ledonc je voyais pas le x10 :+++:
Oui, je suis d'accord avec toi : il y apossibilités.
Tu sais me dire si la formule ne compte pas des doublons genre :
2 2 2 99 et 2 2 2 99
Genre la même "combinaison", mais en changeant de place deux "2".
Pour être sur, si on prend le même truc mais avec le code comprenant 3 chiffres "7") on aurait:
A(2;5) = 25
C(3,5) = 10
Soit 25x10 = 250 possibiltés?
nico253 a écrit:Tu sais me dire si la formule ne compte pas des doublons genre :
2 2 2 99 et 2 2 2 99
Genre la même "combinaison", mais en changeant de place deux "2".
Pour être sur, si on prend le même truc mais avec le code comprenant 3 chiffres "7") on aurait:
A(2;5) = 25
C(3,5) = 10
Soit 25x10 = 250 possibiltés?
J'ai un peu de mal à comprendre ce que tu veux dire...
Ayant choisit les deux places pour les "
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:J'ai un peu de mal à comprendre ce que tu veux dire...
Ayant choisit les deux places pour les "", si on veut que les trois autres chiffres soient pairs, il ne reste que
possibilités toutes distinctes entre elles. Il n'y a pas de "doublon" comme tu dis.
Je voulais dire genre :
222 99
2 2 2 99
2 2 2 99 avec les 2 pas a la même place
nico253 a écrit:Je voulais dire genre :
222 99
2 2 2 99
2 2 2 99 avec les 2 pas a la même place
C'est le même code : lorsque des chiffres sont égaux, on ne tient pas compte de l'ordre : 22 299 désigne un seul et unique code parmi les 12 500 codes possibles.
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:C'est le même code : lorsque des chiffres sont égaux, on ne tient pas compte de l'ordre : 22 299 désigne un seul et unique code parmi les 12 500 codes possibles.
Oui oui tout à fait d'accord, mais est-ce que dans nos calculs ça en tient compte que c'est le même?
Est-ce que dans les 125 on a pas justement 6 fois le même?
nico253 a écrit:Oui oui tout à fait d'accord, mais est-ce que dans nos calculs ça en tient compte que c'est le même?
Est-ce que dans les 125 on a pas justement 6 fois le même?
Je t'ai dit que non :we:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
