Algorithme terminale ES, rentrée !!
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
soso10
- Membre Naturel
- Messages: 29
- Enregistré le: 22 Fév 2013, 12:12
-
 par soso10 » 01 Jan 2014, 17:41
par soso10 » 01 Jan 2014, 17:41
Bonjour, j'ai un exercice à rendre pour la rentrée mais je ne comprends pas le 1b).
Serait-il possible qu'on me mette sur les bonnes pistes s'il vous plait ? Merci d'avance.
Voici l'énoncé :
On pose : S = 1 +
^2 + ... + (\frac{4}{3})^n)
.
On se propose de résoudre le problème suivant : trouver la plus petite valeur de n tel que S soit supérieur à A, où A est un nombre donné à l'avance. On considère l'algorithme suivant :
Saisir A
n prend la valeur 0
S prend la valeur 1
Tant que S < A faire
n prend la valeur n+1
S prend la valeur S +
^n)
Fin Tant que
Afficher n
Afficher S
1a) Pour A = 4, expliquez le déroulement de cet algorithme. b) Indiquez la plus petite valeur de n telle que S soit supérieur à 4 et précisez à quel tour de la boucle "Tant que" cette valeur est obtenue.2a) Faites le calcul à la main pour A = 10
b) Indiquez la plus petite valeur de n telle que S soit supérieur à 4 et précisez à quel tour de la boucle "Tant que" cette valeur est obtenue.2a) Faites le calcul à la main pour A = 10  b) Vérifiez sur votre calculatrice ou votre ordinateur que l'algorithme précédent donne le même résultat.
b) Vérifiez sur votre calculatrice ou votre ordinateur que l'algorithme précédent donne le même résultat.J'ai vérifié avec le logiciel Algobox, mes résultats sont corrects. Par contre, pourquoi lors du lancement, lorsque je teste A = 4 et A = 10 à quoi correspondent les nombres que j'ai mis en gras ?
***Algorithme lancé***
Entrer a : 4
24.1111111 ***Algorithme terminé***
***Algorithme lancé***
Entrer a : 10
513.855967 ***Algorithme terminé***
 par busard_des_roseaux » 01 Jan 2014, 21:48
par busard_des_roseaux » 01 Jan 2014, 21:48
bonjour,
il te faut écrire un programme qui effectue la somme pour "voir" les résultats.
le cours dit:
^{n+1}-1}{\frac{4}{3}-1}>A)
^{n+1}> \frac{1}{3}A+1)
on passe au logarithme népérien
-ln(3)})
}{(2ln(2)-ln(3))}- 1)
dès que cette condition est vérifiée, la somme est supérieure à A.
-
soso10
- Membre Naturel
- Messages: 29
- Enregistré le: 22 Fév 2013, 12:12
-
 par soso10 » 01 Jan 2014, 22:19
par soso10 » 01 Jan 2014, 22:19
Je ne comprend pas par quels procédés vous passez de la somme au logarithme..
Plus en détails, est-ce que cela peut être bon pour un début ? (c'est comme cela qu'on faisait en cours avec les sommes)
S =

> A
=

> A
=

> A
=

> A
= -

 par busard_des_roseaux » 01 Jan 2014, 22:25
par busard_des_roseaux » 01 Jan 2014, 22:25
tu as une erreur de signe à l'avant dernière ligne. sinon, ce qui est écrit
équivaut à mon calcul
il faut parenthèser autour de
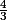
on passe au logarithme népérien que tout à la fin. le logarithme népérien
est une fonction qui permet d'écrire
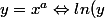= a \, ln(x))
pour calculer l'exposant

enfin , le tutoiement est de rigueur sur les phorums.
-
soso10
- Membre Naturel
- Messages: 29
- Enregistré le: 22 Fév 2013, 12:12
-
 par soso10 » 01 Jan 2014, 23:08
par soso10 » 01 Jan 2014, 23:08
Pour avoir le signe positif, est-ce qu'il faut développer à ce stade ?
^{n+1}}))
> A
Du coup cela ferai :

> A ? Ou alors :
^{n+1}})
> A ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités


