Algorithme exercice

[ins.as]

soit une fonction f définie sur un intervalle [a;b]; on souhaite évaluer les variations de cette fonction. Pour cela, on compare 101 valeurs successives de la fonction f .
On considère l'algorithme suivant :

Entrée : Les réels a et b .
Traitement : Calculer p = b - a / 100 .
Affecter la valeur a à x, 0 à n.
Tant que x < b
Si f (x+p) ;) f(x)
Affecter la valeur n+1 à n,
Affecter la valeur x+p à x.
Sortie : Afficher n .

a - Que représente p ?
b - Combien de fois l'algorithme va t-il effectuer un teste conditionnel ?
c - Si la fonction f est croissante, que vaudra n à la sortie de l'algorithme ?
d - Si la fonction est décroissante, que vaudra n à la sortie de l'algorithme ?
e - Indira utilise cet algorithme. Elle trouve n = 48. Que peut-elle en conclure quant aux variations de f ?
f - Laurent essaye à son tour avec une autre fonction définie sur l'intervalle [0;1] et trouve n = 0 .
Il s'exclame : " ma fonction est décroissante sur [0;1]." " Ce n'est pas sûr et certain" rétorqua Indira.
Qui a raison ? justifier.

Je n'arrive pas a comprendre cet exercice ... :cry:

[fatal_error]

salut,

as tu essayé de dérouler l'algorithme
Si je te donne a=2 et b=20, et f(x) = x^2
qu'est-ce que fait l'algorithme?

[ins.as]

Alors là ... En fait je ne comprends pas ce que fait ' n ' ici ... Je ne comprends vraiment rien aux algorithmes :triste: ... ( Merci pour ton aide :happy2: )

[fatal_error]

Entrée : Les réels a et b .
a=2
b=20
Traitement : Calculer p = b - a / 100 .
p=(20-2)/100=0.18
Affecter la valeur a à x
x=a donc x=2
Affecter la valeur 0 à n.
n=0
Tant que x < b
x=2, or 2<20, donc on rentre dans la boucle
Si f (x+p) ;) f(x)
f(x+p)=f(2+0.18)=(2+0.18)^2
f(x)=f(2)=2^2
On a f(x+p)>f(x), donc on rentre dans la boucle Si
Affecter la valeur n+1 à n
n=0+1=1
Affecter la valeur x+p à x.
x=x+0.18=2.18
Et on remonte au tant que avec x qui vaut désormais 2.18

A toi de faire la suite

[peter45]

Ton énoncé comporte une erreur , il faut lire p = (b - a) / 100 , ce qui correpsond au partage de ton intervalle de définition en 100 subdivisions, p est le pas de calcul.
Cet algorithme, en partageant l'intervalle de définition en 100 subdivisions, recherche le maximum de la fonction sur un intervalle de longueur .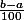
Personnellement, je trouve l'exo un peu brut de dec...