Algorithme de calcul des coefficients de Bézout
18 messages
- Page 1 sur 1
Algorithme de calcul des coefficients de Bézout
Bonsoir,
J'ai un exercice que je ne comprends pas du tout :/
Voici le lien de l'exercice : http://www.ilemaths.net/forum-sujet-524293.html
Merci d'avance et bonne fin de journée !
Édit : je n'ai pas réécris tout l'exercice, ça m'a pris du temps et j'en manque car j'ai énormément de travail à faire :/
J'ai un exercice que je ne comprends pas du tout :/
Voici le lien de l'exercice : http://www.ilemaths.net/forum-sujet-524293.html
Merci d'avance et bonne fin de journée !
Édit : je n'ai pas réécris tout l'exercice, ça m'a pris du temps et j'en manque car j'ai énormément de travail à faire :/
Bon, le mieux est donc d'aller se documenter, de lire quelque manuel scolaire ou sites Internets qui expliquent ce qu'est un PGDC et comment ceci est relié à l'algorithme d'Euclide.
Par contre, dans le début de l'énoncé on indique de noter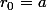 et
et 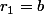 .
.
On y lit aussi que l'on cherche les suite u et v telles que .
.
Donc, pour (niveau
(niveau 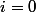 ) , quelles doivent être les valeurs de
) , quelles doivent être les valeurs de  et
et  pour que l'on ait :
pour que l'on ait :  ?
?
Par contre, dans le début de l'énoncé on indique de noter
On y lit aussi que l'on cherche les suite u et v telles que
Donc, pour
C.Ret a écrit:Bon, le mieux est donc d'aller se documenter, de lire quelque manuel scolaire ou sites Internets qui expliquent ce qu'est un PGDC et comment ceci est relié à l'algorithme d'Euclide.
Par contre, dans le début de l'énoncé on indique de noteret
.
On y lit aussi que l'on cherche les suite u et v telles que.
Donc, pour(niveau
) , quelles doivent être les valeurs de
et
pour que l'on ait :
?
a = b.q + r
r = a - b.q
r0 = 1.a - q.b
Donc uo = 1 et vo = q ?
Kadok a écrit:Donc uo = 1 et vo = q ?
Si j'utilise
Or on cherche à avoir
Au niveau 0, on n'a pas encore fait de divison euclidienne, c'est juste une façon de poser les initiales du problème pour trouver les élément initiaux des suite u et v.
Il suffit donc d'avoir
On a alors bien
Même question, on veux que
Sachant que
Kadok a écrit:quand
= 0 et
= 1.
Correct ?
Oui, c'est bien comme cela de s'initie les deux suites.
Et alorsquand
= 1 et
= -q
Par contre, là non ce n'est tout à fait cela. Mais, c'est l'idée.
Je propose de construire un tableau afin de respecter les notations et indice imposé par l'énoncé :
- Code: Tout sélectionner
i u v r = a.u + b.v = r.q + r
0 1 0 r0= a = r1.q1 + r2 = b.q + r
1 0 1 r1= b = r2.q2 + r3
2 ? ? r2= a.u2 + b.v2 = r3.q3 + r4
3 ? ? r3= a.u3 + b.v3 = r4.q4 + r5
4 ? ? r4= ...
Pour le moment on ne conait pas les u et v; on va les déterminer.
Pour le moment on connait u0=1, v0=0, u1=0, v1=1, r0=a et r1=b
Cherchons les relations liant
Prenons par exemple r4. D'après notre tableau on a r2 = r3.q3 + r4. (cf. ligne i=2)
On peut donc en déduire que r4 = ... ?
Kadok a écrit:D'accord, donc d'après le tableau, on peut déduire que
r4 = a.u4 + b.v4 = r5.q5 + r6
Oui c'est vrai, mais ce que l'on cherche c'est exprimer r4 en fonction de r3 et r2.
Car on nous demande d'exprimer r_{i+2} en fonction de r_{i+1} et r_{i}.
Remarque à partir de ta réponse, cela fonctionne aussi : r6 = r4 - q5.r5
On peut même généraliser:
Tu es d'accord ?
Kadok a écrit:J'ai trouvé
Et
C'est ça.
Sachant que les q_i sont les quotients (c'est à dire les parties entières des rapports
- Code: Tout sélectionner
i u v r q
0 1 0 a
1 0 1 b q1=E(a/b)
2 1 -q1 a-b.E(a/b) q2=E(b/(a-b.E(a/b)))
3 -q2 1-q1.q2 -a.q2+b.(1-q1.q2) q3=E((a-b.E(a/b))/(-a.q2+b.(1-q1.q2)))
etc.
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
