Algo
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 15 Aoû 2015, 12:14
par chan79 » 15 Aoû 2015, 12:14
Salut
Si on fait l'équivalent avec un tableur, on a:

on voit que b-a est plus petit que 0.001 lorsque a et b prennent les valeurs en rouge,
qui sont bien égales à tes deux fractions.Pour avoir une précision au millième de la solution, il faut continuer un peu.
On voit que cette solution

vérifie
1,490 <

<1,491
-
Carlalprs
- Membre Naturel
- Messages: 45
- Enregistré le: 27 Avr 2015, 19:42
-
 par Carlalprs » 15 Aoû 2015, 12:23
par Carlalprs » 15 Aoû 2015, 12:23
chan79 a écrit:Salut
Si on fait l'équivalent avec un tableur, on a:

on voit que b-a est plus petit que 0.001 lorsque a et b prennent les valeurs en rouge,
qui sont bien égales à tes deux fractions.Pour avoir une précision au millième de la solution, il faut continuer un peu.
On voit que cette solution

vérifie
1,490 <

<1,491
Bonjour, d'accord merci mais ça veut dire qu'avec mes deux fractions j'ai une précision au 1/100 près ?
-
Carlalprs
- Membre Naturel
- Messages: 45
- Enregistré le: 27 Avr 2015, 19:42
-
 par Carlalprs » 15 Aoû 2015, 14:17
par Carlalprs » 15 Aoû 2015, 14:17
Landstockman a écrit:Comment tu as obtenu cette valeur ?
donc pour la précision, c'est à 1/100 près?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 15 Aoû 2015, 14:41
par chan79 » 15 Aoû 2015, 14:41
Carlalprs a écrit:donc pour la précision, c'est à 1/100 près?
tu as trouvé:
1,4892578125 <

<1,490234375
Comme 1.490234375-1.489257813=0.0009765625, on est sûr que l'écart entre 1,49 et

est plus petit que 1/1000.
1,49 est donc bien une valeur approchée au millième.
A noter que l'encadrement ci-dessus ne nous permet pas de connaître le chiffre des centièmes de

.
-
Carlalprs
- Membre Naturel
- Messages: 45
- Enregistré le: 27 Avr 2015, 19:42
-
 par Carlalprs » 15 Aoû 2015, 14:48
par Carlalprs » 15 Aoû 2015, 14:48
chan79 a écrit:tu as trouvé:
1,4892578125 <

<1,490234375
Comme 1.490234375-1.489257813=0.0009765625, on est sûr que l'écart entre 1,49 et

est plus petit que 1/1000.
1,49 est donc bien une valeur approchée au millième.
A noter que l'encadrement ci-dessus ne nous permet pas d'être sûr du chiffre des centièmes de

.
D'accord merci beaucoup

-
Landstockman
- Membre Relatif
- Messages: 188
- Enregistré le: 11 Aoû 2015, 07:22
-
 par Landstockman » 15 Aoû 2015, 16:06
par Landstockman » 15 Aoû 2015, 16:06
chan79 a écrit:Salut
Si on fait l'équivalent avec un tableur, on a:

on voit que b-a est plus petit que 0.001 lorsque a et b prennent les valeurs en rouge,
qui sont bien égales à tes deux fractions.Pour avoir une précision au millième de la solution, il faut continuer un peu.
On voit que cette solution

vérifie
1,490 <

<1,491
Je pense qu'il faut faire comme le dit chan79, mais dans l'exercice, on demande de rajouter une ligne a la fin...
Du coup...
-
Carlalprs
- Membre Naturel
- Messages: 45
- Enregistré le: 27 Avr 2015, 19:42
-
 par Carlalprs » 15 Aoû 2015, 16:10
par Carlalprs » 15 Aoû 2015, 16:10
Landstockman a écrit:Je pense qu'il faut faire comme le dit chan79, mais dans l'exercice, on demande de rajouter une ligne a la fin...
Du coup...
mais donc quand je rajoute ma ligne : (a+b)/2 c'est faux?
-
Landstockman
- Membre Relatif
- Messages: 188
- Enregistré le: 11 Aoû 2015, 07:22
-
 par Landstockman » 15 Aoû 2015, 16:11
par Landstockman » 15 Aoû 2015, 16:11
Sincèrement, je ne sais pas trop...
Chan79 ?
-
Carlalprs
- Membre Naturel
- Messages: 45
- Enregistré le: 27 Avr 2015, 19:42
-
 par Carlalprs » 15 Aoû 2015, 16:12
par Carlalprs » 15 Aoû 2015, 16:12
Landstockman a écrit:Sincèrement, je ne sais pas trop...
Chan79 ?
car je prend le centre de l'intervalle a b
-
Landstockman
- Membre Relatif
- Messages: 188
- Enregistré le: 11 Aoû 2015, 07:22
-
 par Landstockman » 15 Aoû 2015, 16:14
par Landstockman » 15 Aoû 2015, 16:14
Oui c'est vrai...
Du coup ta ligne c'est :
Afficher
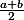
?
-
Carlalprs
- Membre Naturel
- Messages: 45
- Enregistré le: 27 Avr 2015, 19:42
-
 par Carlalprs » 15 Aoû 2015, 16:17
par Carlalprs » 15 Aoû 2015, 16:17
Landstockman a écrit:Oui c'est vrai...
Du coup ta ligne c'est :
Afficher
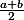
?
oui exacte et j'obtient : 3051/2048 au millième près
-
Landstockman
- Membre Relatif
- Messages: 188
- Enregistré le: 11 Aoû 2015, 07:22
-
 par Landstockman » 15 Aoû 2015, 16:18
par Landstockman » 15 Aoû 2015, 16:18
D'accord :we:
Mais peut être qu'il vaut mieux afficher une valeur décimale...
-
Carlalprs
- Membre Naturel
- Messages: 45
- Enregistré le: 27 Avr 2015, 19:42
-
 par Carlalprs » 15 Aoû 2015, 16:20
par Carlalprs » 15 Aoû 2015, 16:20
Landstockman a écrit:D'accord :we:
Mais peut être qu'il vaut mieux afficher une valeur décimale...
je peux pas mettre approx dans mon algo pour avoir une valeur décimale?
-
Landstockman
- Membre Relatif
- Messages: 188
- Enregistré le: 11 Aoû 2015, 07:22
-
 par Landstockman » 15 Aoû 2015, 16:23
par Landstockman » 15 Aoû 2015, 16:23
[quote=""][/quote]
Pas besoin de l'écrire dans l'algorithme mais pour donner les valeurs arrondis

-
Carlalprs
- Membre Naturel
- Messages: 45
- Enregistré le: 27 Avr 2015, 19:42
-
 par Carlalprs » 15 Aoû 2015, 16:24
par Carlalprs » 15 Aoû 2015, 16:24
Landstockman a écrit:Pas besoin de l'écrire dans l'algorithme mais pour donner les valeurs arrondis

donc approx (a+b)/2 en sortie?
-
Carlalprs
- Membre Naturel
- Messages: 45
- Enregistré le: 27 Avr 2015, 19:42
-
 par Carlalprs » 15 Aoû 2015, 16:26
par Carlalprs » 15 Aoû 2015, 16:26
Carlalprs a écrit:donc approx (a+b)/2 en sortie?
j'obtient donc directement 1,48975 arrondi au millième près c'est ça?
-
Landstockman
- Membre Relatif
- Messages: 188
- Enregistré le: 11 Aoû 2015, 07:22
-
 par Landstockman » 15 Aoû 2015, 16:28
par Landstockman » 15 Aoû 2015, 16:28
Carlalprs a écrit:donc approx (a+b)/2 en sortie?
Non ce n'est pas la peine mais quand on te demande les valeurs donne les valeurs approchées...
Ta machine te donne toujours des valeurs exactes ?
-
Carlalprs
- Membre Naturel
- Messages: 45
- Enregistré le: 27 Avr 2015, 19:42
-
 par Carlalprs » 15 Aoû 2015, 16:29
par Carlalprs » 15 Aoû 2015, 16:29
Landstockman a écrit:Non ce n'est pas la peine mais quand on te demande les valeurs donne les valeurs approchées...
Ta machine te donne toujours des valeurs exactes ?
oui pratiquement
-
Landstockman
- Membre Relatif
- Messages: 188
- Enregistré le: 11 Aoû 2015, 07:22
-
 par Landstockman » 15 Aoû 2015, 16:31
par Landstockman » 15 Aoû 2015, 16:31
C'est quel modèle ? (Simple curiosité hein)

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 15 Aoû 2015, 16:32
par chan79 » 15 Aoû 2015, 16:32
Carlalprs a écrit:je peux pas mettre approx dans mon algo pour avoir une valeur décimale?
Pour la question e, OK pour afficher (a+b)/2 (valeur approchée à 1/1000)
Pour la question f, si on remplace 0.001 par 0.0001 (soit
Tant que b-a>0.0001), la valeur affichée sera une valeur approchée au 1/10000
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 94 invités

