Bonjour/bonsoir pouvez-vous m'aider à résoudre ce problème s'il vous plaît j'ai essayé de le résoudre mais je n'y arrive pas si quelqu'un peut me donner une petite astuce ça pourrait m'aider.
Déterminer m pour que la droite y = mx soit tangente à la parabole y = (x au carré/2)+2
Algèbre droite tangente à la parabole
4 messages
- Page 1 sur 1
Re: Algèbre droite tangente à la parabole
Bonsoir,
on t'a déjà donné des infos ici https://www.ilemaths.net/sujet-algebre-2-833455.html
ce n'est pas correct de poster partout
on t'a déjà donné des infos ici https://www.ilemaths.net/sujet-algebre-2-833455.html
ce n'est pas correct de poster partout
Re: Algèbre droite tangente à la parabole
Soit A(a;b) les coordonnées du point de tangence , dans un repère.
il suffit d'exprimer que le point A appartient aux deux courbes d'équation
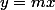 et
et =\dfrac{x^2}{2}+2)
et que le coefficient directeur m de la droite est égal au nombre dérivé de f en a.
soit trois inconnues a,b et m et trois conditions.
il suffit d'exprimer que le point A appartient aux deux courbes d'équation
et que le coefficient directeur m de la droite est égal au nombre dérivé de f en a.
soit trois inconnues a,b et m et trois conditions.
Re: Algèbre droite tangente à la parabole
Variante tardive :
Il suffit de déterminer m tel que la droite et la parabole se coupent en 2 points confondus soit les valeurs de
m qui annulent le discriminant de l'équation du second degré (en x) :

Il suffit de déterminer m tel que la droite et la parabole se coupent en 2 points confondus soit les valeurs de
m qui annulent le discriminant de l'équation du second degré (en x) :
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
