Aire et parabole
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
farator
- Membre Irrationnel
- Messages: 1319
- Enregistré le: 16 Déc 2006, 14:03
-
 par farator » 13 Oct 2007, 14:28
par farator » 13 Oct 2007, 14:28
Bonjour à tous. Voici un dm utilisant la méthode des rectangles.

Je pense qu'il faut tout d'abord définir les suites (Un) et (Vn) par la donnée de leur terme général ?
J'ai pensé pour (Un) à
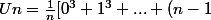^3])
?
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 13 Oct 2007, 14:44
par rene38 » 13 Oct 2007, 14:44
Bonjour
Ton titre : attention, la courbe n'est pas une parabole.
J'ai pensé pour (Un) à

Oui pour le

qui est la "largeur" d'un rectangle mais
la hauteur de chaque rectangle n'est pas 1,
c'est l'ordonnée du point de la courbe
dont l'abscisse est 0, 1/n, 2/n, ..., (n-1)/n
Cette hauteur vaut donc

,

, ,

et on peut bien sûr mettre

en facteur commun.
-
farator
- Membre Irrationnel
- Messages: 1319
- Enregistré le: 16 Déc 2006, 14:03
-
 par farator » 13 Oct 2007, 16:16
par farator » 13 Oct 2007, 16:16
Voilà, donc si j'ai bien compris, cela donne :
Un = Largeur x hauteur
Un = abscisse x ordonnée
Un =
^3+(\frac{1}{n})^3+...+(\frac{n-1}{n})^3])
Un =
^3)(0^3)+((\frac{1}{n})^3)(1^3)+...+((\frac{1}{n})^3)((\frac{n-1}{n})^3)])
Un =
(0^3)+(\frac{1}{n^3})(1^3)+...+ (\frac{1}{n^3})((n-1)^3)])
Un =
[((\frac{1}{n})^3)(0^3+1^3+...+(n-1)^3)])
Un =
(\frac{1}{n^3})(0^3+1^3+...+(n-1)^3)])
Un =
[0^3+1^3+...+(n-1)^3])
Voilà, est-ce que c'est bon ??
Je n'ai par contre pas compris pourquoi la hauteur s'arrête à
^3)
??
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 13 Oct 2007, 16:26
par rene38 » 13 Oct 2007, 16:26
Oui, c'est bon.
Je n'ai par contre pas compris pourquoi la hauteur s'arrête à

Regarde le dernier rectangle à droite
(pas le plus haut, celui qui est en-dessous de la courbe :
son coin supérieur gauche a pour abscisse

donc pour ordonnée

qui est donc la "hauteur" du rectangle
et comme on a mis

en facteur ...
La hauteur s'arrêtera à n³ pour l'autre suite (les grands rectangles)
mais qui partira de 1³ et non 0³
-
farator
- Membre Irrationnel
- Messages: 1319
- Enregistré le: 16 Déc 2006, 14:03
-
 par farator » 13 Oct 2007, 16:35
par farator » 13 Oct 2007, 16:35
C'est bon j'ai compris.
Merci René. Je pense savoir faire la suite de l'exercice.
En tout cas merci beaucoup :++:
-
farator
- Membre Irrationnel
- Messages: 1319
- Enregistré le: 16 Déc 2006, 14:03
-
 par farator » 13 Oct 2007, 19:45
par farator » 13 Oct 2007, 19:45
J'ai réussi à montrer que
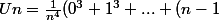^3))
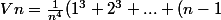^3+n^3))
Ensuite, j'ai réussi à prouver que
^2}{4})
Ainsi,
^2}{4}])
^2}{4}])
Donc,
^2}{4}] \le A \le \frac{1}{n^4}[\frac{n^2(n+1)^2}{4}])
Après, je ne suis pas sûr de la valeur de n. Je pense à 10, en regardant le graphique de l'énoncé.
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 13 Oct 2007, 23:14
par rene38 » 13 Oct 2007, 23:14
Après, je ne suis pas sûr de la valeur de n. Je pense à 10, en regardant le graphique de l'énoncé
Non, relis l'énoncé :
on partage l'intervalle [0 ; 1] en n intervalles de largeur 1/n.
La précision de l'encadrement

sera donc d'autant meilleure que n sera grand, le meilleur résultat étant obtenu en faisant tendre n vers +l'infini et en chechant les limites des 2 suites qui encadrent A.
-
farator
- Membre Irrationnel
- Messages: 1319
- Enregistré le: 16 Déc 2006, 14:03
-
 par farator » 14 Oct 2007, 10:43
par farator » 14 Oct 2007, 10:43
Comme la limite en +infini de ces deux suites est
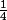
, j'en déduis que

??
-
farator
- Membre Irrationnel
- Messages: 1319
- Enregistré le: 16 Déc 2006, 14:03
-
 par farator » 14 Oct 2007, 12:44
par farator » 14 Oct 2007, 12:44
Cela me semble correspondre avec le graphique. Non ?
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 14 Oct 2007, 13:17
par rene38 » 14 Oct 2007, 13:17
C'est bien ça.
-
farator
- Membre Irrationnel
- Messages: 1319
- Enregistré le: 16 Déc 2006, 14:03
-
 par farator » 14 Oct 2007, 13:22
par farator » 14 Oct 2007, 13:22
merci rene38, c'est super !
:++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités


 qui est la "largeur" d'un rectangle mais
qui est la "largeur" d'un rectangle mais ,
,  , ,
, ,  et on peut bien sûr mettre
et on peut bien sûr mettre  en facteur commun.
en facteur commun. donc pour ordonnée
donc pour ordonnée  qui est donc la "hauteur" du rectangle
qui est donc la "hauteur" du rectangle  en facteur ...
en facteur ... sera donc d'autant meilleure que n sera grand, le meilleur résultat étant obtenu en faisant tendre n vers +l'infini et en chechant les limites des 2 suites qui encadrent A.
sera donc d'autant meilleure que n sera grand, le meilleur résultat étant obtenu en faisant tendre n vers +l'infini et en chechant les limites des 2 suites qui encadrent A.