Aire d'un cube avec ses arêtes.

[M0ustiikos]

Salut,
Je bloque sur un exercice :

"De combien augmente l'aire totale d'un cube lorsque la longeur de chacunes de ses arretes augmente de 50% ?"

Merci de m'éclaircire, moi et les aires : on se comprend pas! :marteau:

[MacManus]

Bonjour !

J'aurais plutôt tendance à parler de " volume " d'un cube.
Soit la longueur d'une arrête du cube. On sait que son volume V est :
V =

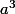
Augmenter de 50%, cela signifie augmenter la longueur de sa moitié, cad de

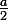
tu vois comment continuer ?

[M0ustiikos]

Donc : V.Total = (a3 x 12) x a/2.

C'est ça ? :hein:

[MacManus]

ah non !
on ajoute "a/2" à "a" : on obtient a + a/2 = 3a/2
ensuite on calcule le nouveau volume :zen:

[M0ustiikos]

Ha oui !

Mais pour le volume total du cube, on doit faire 3a/2 x 12 ?
Puisqu'il y a 12 arrêtes. ?!

[M0ustiikos]

Ha mais nan ! ><

Suis-je bête ! :P mon message précèdent est complètement HS..

Donc le volume totale d'un cube lorsque la longueur de chacune de ses arêtes augmente de 50% est de 3a/2.

Si c'est ça, c'est tout c** finalement :o

[MacManus]

et non !
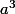
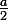
V = , donc si tu augmentes de la longueur a , le volume devient :
V = = ?