J'ai besoin d'un petit coup de pouce sur cet énoncé:
il faut démontrer que
a4 + a3 + a2 + a + 1 = 0
avec a= exp(j2pi/5)
si ca peut aider dans l'exercice j'ai deja démontré que 1/2(a+1/a)=cos(2pi/5)
et a5-1=0
mais pour l'autre je galère... :(
merci pour l'aide
Aidez moi (trigo)
8 messages
- Page 1 sur 1
et j la dedans y deviens quoi?.
sinon je ne sais pas si c'est valable
mais en factorisant a je peux remplacer a+1/A et substituer avec la formule d'euler pour revenir a ca
2 + exp(j8pi/5) + 2exp(j4pi/5) + exp(j 2pi/5)
mais apres je suis bloqué je vais tenter de redévelopper avec les puissance pour voir...
sinon je ne sais pas si c'est valable
mais en factorisant a je peux remplacer a+1/A et substituer avec la formule d'euler pour revenir a ca
2 + exp(j8pi/5) + 2exp(j4pi/5) + exp(j 2pi/5)
mais apres je suis bloqué je vais tenter de redévelopper avec les puissance pour voir...
soit
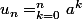
Supposons
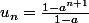
testons
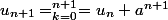
Même dénominateur
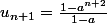
Quant au j, si le probleme c'est que a est un complexe, il faut alors justifier que
 = a^{n+1}-a^{n+2})
Et ca c'est du cours.
PS ( pour a différent de 1... )
Edit: apres je fais que proposer, tu prends tu prends pas c'est ton choix! dailleurs je pense que c'est pas ca qui est attendu.
Supposons
testons
Même dénominateur
Quant au j, si le probleme c'est que a est un complexe, il faut alors justifier que
Et ca c'est du cours.
PS ( pour a différent de 1... )
Edit: apres je fais que proposer, tu prends tu prends pas c'est ton choix! dailleurs je pense que c'est pas ca qui est attendu.
la vie est une fête 
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 94 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
