[Terminale] Aide sur fonction exponentielle
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
iima
- Messages: 7
- Enregistré le: 04 Jan 2009, 00:41
-
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 04 Jan 2009, 00:49
par XENSECP » 04 Jan 2009, 00:49
C'est moi ou il manque "ce que tu as fait" ?
-
iima
- Messages: 7
- Enregistré le: 04 Jan 2009, 00:41
-
 par iima » 04 Jan 2009, 00:56
par iima » 04 Jan 2009, 00:56
j'ai fais la courbe et le tableau :hum:
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 04 Jan 2009, 01:13
par Clembou » 04 Jan 2009, 01:13
C'est cool ! On voudrait aussi voir le reste si ça te dérange pas :++:
-
iima
- Messages: 7
- Enregistré le: 04 Jan 2009, 00:41
-
 par iima » 04 Jan 2009, 01:18
par iima » 04 Jan 2009, 01:18
je suis bloquée les autres questions je ne sais pas :doh:
-
Huppasacee
- Membre Complexe
- Messages: 2635
- Enregistré le: 22 Jan 2008, 23:05
-
 par Huppasacee » 04 Jan 2009, 02:06
par Huppasacee » 04 Jan 2009, 02:06
alors , comment calculerais tu la dérivée de cette fonction ?

sous quelle forme peux tu décomposer cette fonction ?
avec du u , du v etc ..
je commencerais en disant
posons u = t
et v =
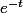
alors f(x) = ...
-
iima
- Messages: 7
- Enregistré le: 04 Jan 2009, 00:41
-
 par iima » 04 Jan 2009, 04:05
par iima » 04 Jan 2009, 04:05
f' (t) = 8.25 * 1* -
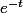
car
u= t v=
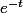
u'= 1 v'= -
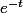
-
Huppasacee
- Membre Complexe
- Messages: 2635
- Enregistré le: 22 Jan 2008, 23:05
-
 par Huppasacee » 04 Jan 2009, 10:43
par Huppasacee » 04 Jan 2009, 10:43
Il te manque une partie de la dérivée
tu sais que la dérivée de u*v est u'v + u v'
-
iima
- Messages: 7
- Enregistré le: 04 Jan 2009, 00:41
-
 par iima » 04 Jan 2009, 13:31
par iima » 04 Jan 2009, 13:31
u = t v =
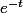
u' = 1 v'= -
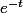
f'(t) = 8.5 * (u'v + uv')
f'(t) = 8.25 * (1 *
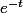
+ t * -
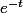
)
f'(t) = 8.25 * (
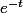
+ t * -
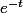
)
f'(t) = 8.25
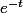
+ 8.25t * -
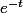
f'(t)= 8.25
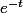
* (1-t)
-
iima
- Messages: 7
- Enregistré le: 04 Jan 2009, 00:41
-
 par iima » 04 Jan 2009, 16:36
par iima » 04 Jan 2009, 16:36
8.25e^-t > 0 car une fonction exp est toujours positive
1-t > 0 donc t>1 soit 1-t > 0 sur [0;1]
1-t < 0 sur [1;4]

y = f'(0)(x-0) + f(0) soit y = 8.25(x-0) + 0 = 8.25x
y = f'(1)(x-1) + f(1) soit y = 0(x-0) +

=

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 83 invités





