J'ai un dm pour la rentrée et j'ai déjà bien avancé il me reste plus qu'un exercice que je n'arrive même pas à commencer...
le sujet est le suivant :
Soit la suite (Un) définie par U1=1 et Un+1= (nUn+4)/(n+1) pour tout n>= a 1
1) conjecturez puis démontrez l'expression de Un en fonction de n
2) déterminer alors la limite de la suite (Un)
Aide pour un Dm sur les suites! Merci
9 messages
- Page 1 sur 1
Re: Aide pour un Dm sur les suites! Merci
Tout le problème est la je n'arrive pas à en trouver !
J'ai essayer de calculer les premiers termes pour voir si elle était géométriques ou arithmétiques ou autre mais je n'arrive pas à trouver de liens entre les termes...
J'ai essayer de calculer les premiers termes pour voir si elle était géométriques ou arithmétiques ou autre mais je n'arrive pas à trouver de liens entre les termes...
Re: Aide pour un Dm sur les suites! Merci
Bon allez je te donne le coup de pouce quand même...
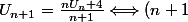U_{n+1} = nU_n+4)
Du coup en posant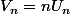 tu tombes sur de l'arithmétique simple et le tour est joué
tu tombes sur de l'arithmétique simple et le tour est joué 
Du coup en posant
Re: Aide pour un Dm sur les suites! Merci
D'accord donc du coup je tombe sur
Vn+1 = Vn + 4
Mais je ne vois pas très bien en quoi cela peut démontrer que Un est arithmétique
Ici on démontre que Vn est arithmétique...
Ou sinon il faudrait enlever le n+1 à Vn+1 pour pouvoir remplacer Vn par nUn et passer le n de l'autre côté pour avoir Un = quelque chose
Mais je ne sais pas comment faire
Vn+1 = Vn + 4
Mais je ne vois pas très bien en quoi cela peut démontrer que Un est arithmétique
Ici on démontre que Vn est arithmétique...
Ou sinon il faudrait enlever le n+1 à Vn+1 pour pouvoir remplacer Vn par nUn et passer le n de l'autre côté pour avoir Un = quelque chose
Mais je ne sais pas comment faire
Re: Aide pour un Dm sur les suites! Merci
Sérieusement ? Vn est arithmétique donc tu connais son expression en fonction de n et tu conclus avec Un = Vn/n .... !!!
Re: Aide pour un Dm sur les suites! Merci
Et bien oui! Désolée je cherchais la complication !
J'ai une dernière question, je dois conjecturer puis démontrer
Donc en conjecture je mets seulement le résultat final sans explications et puis pour démontrer je fais tout ce qu'on a fait avec Vn=nUn etc... ?
J'ai une dernière question, je dois conjecturer puis démontrer
Donc en conjecture je mets seulement le résultat final sans explications et puis pour démontrer je fais tout ce qu'on a fait avec Vn=nUn etc... ?
Re: Aide pour un Dm sur les suites! Merci
Par contre on sait que Vn est arithmétique de raison 4 mais on ne connaît pas son premier terme
Donc on utilise :
Vn = Vp + (n-p) *4 ?
Ce qui nous donne
Un =(Vp+(n-p)*4)/n ?
Donc on utilise :
Vn = Vp + (n-p) *4 ?
Ce qui nous donne
Un =(Vp+(n-p)*4)/n ?
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 108 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
