Aide fonciton ensemble de définition

[Anonyme]

Bonjour je rentre cette année en Terminale S et j'avoue aovoir oublié pratiquement tout le programme de l'année derniere...

Est ce que ça serait possible de me dire comment on calcule l'ensmeble de définition et de dérivabilité d'une fonction?

Merci beaucoup

[Nightmare]

Bonjour

Je suppose que tu as jeté ton cours de maths de l'année derniére .. c'est trés bien surtout quand on l'a entiérement oublié, bonne solution :triste:

L'ensemble de définition d'une fonction c'est l'ensemble des valeurs qui ont une image par f
L'ensemble de dérivabilité d'une fonction c'est l'ensemble des réels a pour lesquelles le nombre dérivé de f en a existe (en gros l'ensemble de définition de la dérivée, mais attention, ne jamais dériver puis donner l'ensemble de dérivabilité, dabord donner cet ensemble puis dériver)

:happy3:
Jord

[S@m]

Ce qui devient compliqué, c'est lorsque tu dérives des fonctions composées, ou l'intervalle de derivabilité est certes plus ardu a trouver (surtout pour certaine) mais selon ma prof de maths,c 'est pas bien grave pour l'instant d'avoir oublier ça (je parle de le ça que je viens d'expliquer...les infos de Nightmare sont en revanche indispensables :marteau: )

[Nightmare]

Bonjour Sam :happy3:

De toute façon ici je ne pense pas que ce soit un oubli puisque la personne vient de rentrer en terminale, or la dérivé d'une composé ce voit justement en terminale

:happy3:
Jord

[julian]

Je te donnerai juste qqes exemples pour t'aider:les seuls problèmes que tu pourras rencontrer ce sera avec des par exemple ou des fractions,sachant que pour celles-ci il est impossible de diviser par 0!
si tu as besoin de bcp d'exemples,je peux tjr t'en donner,mais normalement ton prof va reprendre un peu le programme de 1ère,du moins le résumer (tous les élèves n'ont pas forcément les bases nécessaires en arrivant en terminale :marteau: ).
Amicalement.
Pour Nightmare:je crosi pourtant avoir vu un peu çà l'année dernière quand on avait une fonction ,
tu paralis surement de qqe chose de plus complexe... :hein:

[Nightmare]

Oui mais bon ça c'est un jeux d'enfant que d'étudier les fonctions sous la forme u(ax+b) :lol3: :ptdr:

[phenomene]

Pour Nightmare:je crosi pourtant avoir vu un peu çà l'année dernière quand on avait une fonction ,
tu paralis surement de qqe chose de plus complexe... :hein:

Oui, la dérivation de dans le cas particulier où est une fonction affine (et une fonction dérivable bien sûr) est au programme de première scientifique ; le cas général avec dérivable quelconque ne se voit qu'en terminale (et l'idée de la démonstration de la formule de dérivation composée est explicitement au programme, l'idée seulement, pas les détails).

[julian]

merci à vous. :++:
vivement que je vois tout çà pour être disons moins "largué" parfois sur ce bô forum. :briques: :briques: :ptdr: :ptdr:

[allomomo]

Salut,

Des fois il y a des pièges,

Par exemple, , f est définie sur 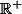alors que sa dérivée est définie : le zéro n'est pas compris car : la fonction racine carré admet une tangente verticale en x=0, ce qui veut dire que la limite de la fonction racine carrée lorsque x tend vers 0 est infinie ( non finie = pas un nombre)


[Cours terminale : dérivation :: tout premier cours lol]

[S@m]

OUais ca encore ça va c'est surtout en effet pour les fonction de type u°v je trouve...en tout cas pour le programme de premiere