Aide devoir etude de fonctions
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Kameron
- Membre Naturel
- Messages: 35
- Enregistré le: 10 Juin 2006, 23:25
-
 par Kameron » 11 Juin 2006, 01:56
par Kameron » 11 Juin 2006, 01:56
Bonjour,
J'ai ce devoir à rendre demain et j'avoue que je suis un peu perdu... Je sais qu'il est long, c'est pourquoi une aide serait vraiment appréciable.
Je suis perdu à partir de la question 3) :triste:

Merci d'avance si vous avez le courage de m'aider :triste:
-
Nicolas_75
- Membre Rationnel
- Messages: 919
- Enregistré le: 29 Aoû 2005, 11:42
-
 par Nicolas_75 » 11 Juin 2006, 07:28
par Nicolas_75 » 11 Juin 2006, 07:28
Bonjour,
Les premières questions de chaque partie sont très simples.
Tu en es où exactement ?
Nicolas
-
Kameron
- Membre Naturel
- Messages: 35
- Enregistré le: 10 Juin 2006, 23:25
-
 par Kameron » 11 Juin 2006, 07:39
par Kameron » 11 Juin 2006, 07:39
Je suis à la trois de la Partie A, et je n'ais pas entamé la B :marteau:
Au moins on est sur que Einstein avait raison, dumoins concernant mon niveau en maths, en disant que les humains sont stupides :hein:
Si tu pouvais m'aidez, ce serait sympa :)
-
Nicolas_75
- Membre Rationnel
- Messages: 919
- Enregistré le: 29 Aoû 2005, 11:42
-
 par Nicolas_75 » 11 Juin 2006, 07:53
par Nicolas_75 » 11 Juin 2006, 07:53
A.1. : qu'as-tu trouvé ?
B.1.a : il suffit de calculer... montre tes calculs...
B.1.b : prends x=y=0
-
Kameron
- Membre Naturel
- Messages: 35
- Enregistré le: 10 Juin 2006, 23:25
-
 par Kameron » 11 Juin 2006, 07:59
par Kameron » 11 Juin 2006, 07:59
Pour les tableaux de variations on a:
si a<0 => croissante puis decroissante de maxima 1
si a>0 => decroissante puis croissante de maxima 1
si a=0 => constante y=1
pour la B1a et B1b je vais essayer.
Je pense que je vais surtout avoir besoin de l'aide pour la 1d et 1e en ce qui concerne le 1).
Merci pour tes réponses :)
-
Kameron
- Membre Naturel
- Messages: 35
- Enregistré le: 10 Juin 2006, 23:25
-
 par Kameron » 11 Juin 2006, 08:09
par Kameron » 11 Juin 2006, 08:09
Mais pas contre pour la A3 comment démontrer la bijection? et g-1 a? :doh:
-
Nicolas_75
- Membre Rationnel
- Messages: 919
- Enregistré le: 29 Aoû 2005, 11:42
-
 par Nicolas_75 » 11 Juin 2006, 08:11
par Nicolas_75 » 11 Juin 2006, 08:11
A.1. si a>0 => decroissante puis croissante de
minimum 1
N'oublie pas de calculer les limites.
A.3.Si

, alors
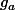
est
strictement croissante sur
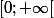
. Or
=1)
et

. Donc
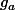
réalise une bijection de
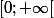
sur

.
Soit

et

=y)




ne me semble pas très loin.
N'oublie pas le cas

.
Pour
B., propose d'abord quelque chose.
Sauf erreur.
-
Kameron
- Membre Naturel
- Messages: 35
- Enregistré le: 10 Juin 2006, 23:25
-
 par Kameron » 11 Juin 2006, 08:21
par Kameron » 11 Juin 2006, 08:21
Si j'ai bien compris, pour a<0 c'est quasiment la même chose sauf que la limite en l'infinie tend vers 0, donc cette fois la bijection est vers l''interval [1;0[. Est-ce bien ceci?
Cependant, je ne vois pas en quoi tes équivalences nous mènent à g-1 a :triste: . Je dois être bête :/
-
Nicolas_75
- Membre Rationnel
- Messages: 919
- Enregistré le: 29 Aoû 2005, 11:42
-
 par Nicolas_75 » 11 Juin 2006, 08:25
par Nicolas_75 » 11 Juin 2006, 08:25
Pour a 0.
A quoi servent mes équivalences ? A trouver

. En effet, la
définition de

n'est-elle pas, à peu de choses près :
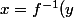 \Longleftrightarrow y=f(x))
?
Si tu te répètes que tu es bête, c'est sûr que tu ne vas aller bien loin. Dis-toi plutôt : "je vais y arriver". D'ailleurs, ce que tu as dit sur a < 0 montre bien que tu comprends.
-
Nicolas_75
- Membre Rationnel
- Messages: 919
- Enregistré le: 29 Aoû 2005, 11:42
-
 par Nicolas_75 » 11 Juin 2006, 08:27
par Nicolas_75 » 11 Juin 2006, 08:27
Tu as fait une petite faute de frappe. Pour a < 0, c'est ]0;1], et non pas [1;0[. :id:
-
Nicolas_75
- Membre Rationnel
- Messages: 919
- Enregistré le: 29 Aoû 2005, 11:42
-
 par Nicolas_75 » 11 Juin 2006, 08:30
par Nicolas_75 » 11 Juin 2006, 08:30
Pour être clair, pour

, je trouve :

c'est-à-dire, et c'est la même chose :
 EDIT
EDIT : Plus précisément :

-
Nicolas_75
- Membre Rationnel
- Messages: 919
- Enregistré le: 29 Aoû 2005, 11:42
-
 par Nicolas_75 » 11 Juin 2006, 08:32
par Nicolas_75 » 11 Juin 2006, 08:32
Pour tracer

et

, tu as deux méthodes :
(1) faire un tableau de valeurs, et tracer, comme d'habitude, ou
(2) te souvenir que la courbe représentative de la fonction réciproque est la symétrique de la courbe représentative de la fonction de départ par la symétrie axiale d'axe y=x.
Nicolas
-
Kameron
- Membre Naturel
- Messages: 35
- Enregistré le: 10 Juin 2006, 23:25
-
 par Kameron » 11 Juin 2006, 08:40
par Kameron » 11 Juin 2006, 08:40
Oui en effet j'ai fait une faute de frappe.
Alors si je comprends bien, pour a>0, g-1 a= racine²(ln y/a)?
Et dans le cas a<0, si l'on refait l'équivalence, cela ne nous donnerait-il pas un a négatif dans la racine?
-
Nicolas_75
- Membre Rationnel
- Messages: 919
- Enregistré le: 29 Aoû 2005, 11:42
-
 par Nicolas_75 » 11 Juin 2006, 08:43
par Nicolas_75 » 11 Juin 2006, 08:43
Pour a > 0, relis mes messages ci-dessus.
Pour a < 0, interroge-toi sur le signe de ln(y), lui aussi sous la racine.
-
Kameron
- Membre Naturel
- Messages: 35
- Enregistré le: 10 Juin 2006, 23:25
-
 par Kameron » 11 Juin 2006, 08:47
par Kameron » 11 Juin 2006, 08:47
Excuse moi, mais dans ton edit:
Ne serait-ce pas plutot g-1 a: [0;+infini[ -> [1;+infini[ ? puisque c'est une bijection de [0;+infini[ vers [1;+infini[. Sinon je crains ne pas comprendre :/.
Je cherche pour a<0 maintenant.
-
Nicolas_75
- Membre Rationnel
- Messages: 919
- Enregistré le: 29 Aoû 2005, 11:42
-
 par Nicolas_75 » 11 Juin 2006, 08:50
par Nicolas_75 » 11 Juin 2006, 08:50
Si f est une bijection de I dans J, alors f-1 est une bijection de J dans I. Cf. ton cours.
Pour a > 0

donc

-
Kameron
- Membre Naturel
- Messages: 35
- Enregistré le: 10 Juin 2006, 23:25
-
 par Kameron » 11 Juin 2006, 08:53
par Kameron » 11 Juin 2006, 08:53
Ok j'ai compris.
Excuse moi pour mes questions mais je n'ai fais aucun cours là dessus, à part les bases sur les exponentiels et complexes.
Je cherche g-1 -1, j'espere trouver :)
-
Kameron
- Membre Naturel
- Messages: 35
- Enregistré le: 10 Juin 2006, 23:25
-
 par Kameron » 11 Juin 2006, 08:58
par Kameron » 11 Juin 2006, 08:58
Si j'opère le même raisonnement pour a négatif, je trouve:
-x²= lny ce qui équivaut à x=racine²(-lny) non?
-
Nicolas_75
- Membre Rationnel
- Messages: 919
- Enregistré le: 29 Aoû 2005, 11:42
-
 par Nicolas_75 » 11 Juin 2006, 09:03
par Nicolas_75 » 11 Juin 2006, 09:03
Pour

,
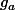
réalise une bijection de
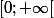
sur
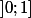

donc

Soit

et

=y)



(or le membre de droite est positif puisque

et
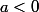
)

Donc :

Sauf erreur.
-
Nicolas_75
- Membre Rationnel
- Messages: 919
- Enregistré le: 29 Aoû 2005, 11:42
-
 par Nicolas_75 » 11 Juin 2006, 09:04
par Nicolas_75 » 11 Juin 2006, 09:04
Kameron a écrit:Si j'opère le même raisonnement pour a négatif, je trouve:
-x²= lny ce qui équivaut à x=racine²(-lny) non?
Tu as raison, mais l'énoncé te demande de trouver la fonction réciproque pour a négatif en général, pas seulement pour a=-1.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités

