Aide développante de cercle

[kmillo]

Bonjour à tout le monde!
Je ne suis pas étudiant mais je cherche une formule. C'est pour du dessin paramétré. Merci d'avance

Le problème:
-J'ai un cercle de diamètre d et un deuxième cercle de diamètre db avec db=d * cos(a) , où "a" est un angle.
-Les deux cercles ont le même centre.
-Une droite OA avec O au centre des deux cercles et A sur db.
-En A je démarre une développante de cercle db.
-B est un point du cercle d à l'intersection de la développante.

Question :
Quel est la formule pour trouver l'angle AÔB?

Exemple pour a =20 °, AÔB =0.8574331269 °

[Ben314]

Salut,
En prenant l'équation "standard" de la développante d'un cercle qu'on peut trouver par exemple là :
https://fr.wikipedia.org/wiki/D%C3%A9ve ... _du_cercle
On a avec (ton deuxième diamètre).
Donc le point est sur le premier cercle lorsque c'est à dire (avec )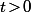
Donc l'angle que tu cherche est tel que :


C'est à dire modulo (tout exprimé en radians, bien sûr)

Example : Radians => Radians .

[kmillo]

Merci beaucoup, sur wiki j'ai regardé mais de là à en déduire quoi que ce soit ...