Aide Concernant Suite numerique [1ere]
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Sirius
- Membre Naturel
- Messages: 24
- Enregistré le: 01 Mai 2007, 10:55
-
 par Sirius » 01 Mai 2007, 11:05
par Sirius » 01 Mai 2007, 11:05
Bonjour,
Je souhaiterai obtenir une aide pour un exercice que je ne comprend pas,
je vous le reporte ci-dessous
On Considere la suite (an) definie par a0=83
a1= 83.215
a2=83.215215
et plus generalement an=83.215(...)215 avec n repetitions du nombres n
a)Montrer que , pour n>/ (superrieur ou egale) 1
an= 83+215/1000+215/1000²+...+215/1000n (n est une puissance de 1000)
b)Exprimer 1/1000+1/1000²+...+1/1000n (n puissance de 1000)
Puis Montrer que pour n>/1 on a
(an)= 83 +215/999 (1- 1/1000n)
Bon alors je pense avoir reussie la a)
j'ai cree une suite Sn, Sn=AN - 83
et pis j'ai conclu
la premiere partie de la question b j'ai mis que que c'etait 0.001...001
avec n repetition de 001 dans la partie décimale
mais je flenche sur (an) = 83+215/999*(1-1/1000n(puissance de mille)
Alors j'aimerai sil vous plait que vous m'expliquiait la methode adequate
Merci D'avance :we:
Sirius
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 01 Mai 2007, 11:27
par Flodelarab » 01 Mai 2007, 11:27
"On reconnait la somme des termes d'une suite géométrique de raison .... et de premier terme ...."
On peut donc appliquer la formule du cours:
-(terme\quad qu'on\quad ecrirait\quad juste\quad apres\quad si\quad on\quad continuait\quad la\quad suite)}{1 - raison})
-
Sirius
- Membre Naturel
- Messages: 24
- Enregistré le: 01 Mai 2007, 10:55
-
 par Sirius » 01 Mai 2007, 12:10
par Sirius » 01 Mai 2007, 12:10
Hum j'avoue ne pas comprendre pourquoi on parle de la somme d'une suite geometrique... Si vous pouvez me repondre Merci ^^ de plus on ne peut pas dire que AN est une suite geometrique puisque une suite geometrique est de formule
Gn= rn(puissance n) * G0
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 01 Mai 2007, 12:18
par Flodelarab » 01 Mai 2007, 12:18
Qu'est ce qu'une suite géométrique ?
Quel lien peut on faire entre 0,001 et 0,000001 et 0,000000001 et.... ?
-
Sirius
- Membre Naturel
- Messages: 24
- Enregistré le: 01 Mai 2007, 10:55
-
 par Sirius » 01 Mai 2007, 12:22
par Sirius » 01 Mai 2007, 12:22
Re Bonjour
c'est simple a chaque progression
Un+1/Un = 0.001
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 01 Mai 2007, 12:25
par Flodelarab » 01 Mai 2007, 12:25
Sirius a écrit:Re Bonjour
c'est simple a chaque progression
Un+1/Un = 0.001
Voilà.
Et la relecture du post #2 ne t'apportes pas satisfaction ?
-
Sirius
- Membre Naturel
- Messages: 24
- Enregistré le: 01 Mai 2007, 10:55
-
 par Sirius » 01 Mai 2007, 12:30
par Sirius » 01 Mai 2007, 12:30
Je dois dire que non je comprend pas *_* J'm'avoue vaincue je vois pas le lien entre ta formule et
an = 83+215/999(1-1/1000 exposant n)
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 01 Mai 2007, 12:35
par Flodelarab » 01 Mai 2007, 12:35
Arretes de te fixer sur le résultat et appliques simplement la formule de la somme des termes d'une suite géométrique.
-
Sirius
- Membre Naturel
- Messages: 24
- Enregistré le: 01 Mai 2007, 10:55
-
 par Sirius » 01 Mai 2007, 12:40
par Sirius » 01 Mai 2007, 12:40
Ok alors
terme initial = a0 = 83
terme qu'on ecrirait juste apres si on continuait la suite = 83 +215+215/1000²+...+215/1000 expo n
1 - la raison
r= 0.001
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 01 Mai 2007, 12:43
par Flodelarab » 01 Mai 2007, 12:43
buzzzzzzzzzzzzzzzz
mauvaise réponse.
ohhhhhhhhhhhhhh
mais vous pouvez relancer la roue
ahhhhhhhhhhhhhh
Ton premier terme n'est pas 83. Car sinon, la suite serait 83 pui 0,083 puis .....
Concentre toi. Et réfléchis entre 2 posts.
-
Sirius
- Membre Naturel
- Messages: 24
- Enregistré le: 01 Mai 2007, 10:55
-
 par Sirius » 01 Mai 2007, 12:47
par Sirius » 01 Mai 2007, 12:47
j'en deduis que ces 215 mais j'arrive pas a me suituer dans la suite *_*
ce qui donne 215-terme suivant
_________________
1- r (r = 0.001)
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 01 Mai 2007, 13:00
par Flodelarab » 01 Mai 2007, 13:00
Pourquoi tu t'arrêtes ?
Continue.
-
Sirius
- Membre Naturel
- Messages: 24
- Enregistré le: 01 Mai 2007, 10:55
-
 par Sirius » 01 Mai 2007, 13:05
par Sirius » 01 Mai 2007, 13:05
hu² apres j'vais mettre une betise et tu va me buzzer j'ai peur :we: :we: :we:
bon alors
215- 0.215
___________
1-0.001
Mais vu que j'arrive pas a me placer dans la bonne suite j'comprend pas l'histoire du terme suivant *_*
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 01 Mai 2007, 13:17
par Flodelarab » 01 Mai 2007, 13:17
Ce serait ça si tu t'arrêtais au premier terme. Mais tu t'arrêtes au rang n... donc le suivant du rang n est ....
-
Sirius
- Membre Naturel
- Messages: 24
- Enregistré le: 01 Mai 2007, 10:55
-
 par Sirius » 01 Mai 2007, 13:20
par Sirius » 01 Mai 2007, 13:20
ca doit donc etre n+1
bon merci pour ton aide j'vais voir de la famille :we: :we: j'vais essayer de y arriver.
mais une simple question pour le termes suivant on laisse pas (n+1)?
n+1 doit etre egale a Un/1000
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 01 Mai 2007, 13:37
par Flodelarab » 01 Mai 2007, 13:37
an= 83+215/1000+215/1000²+...+215/1000n
an= 83+215(1/1000+1/1000²+...+1/1000^n)
an= 83+215(10^-3+10^-6+...+10^-3n)
an= 83+215(10^-3+10^-6+...+10^-3n)

On reconnait la somme des termes d'une suite géométrique de raison 10^-3 et de premier terme 10^-3
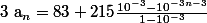
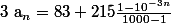
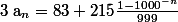
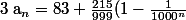)
-
Sirius
- Membre Naturel
- Messages: 24
- Enregistré le: 01 Mai 2007, 10:55
-
 par Sirius » 01 Mai 2007, 17:09
par Sirius » 01 Mai 2007, 17:09
Merci pour tout Miss/Mister :we: Surtout parceque grace a toi j'ai compris :zen:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
