Affixes des sommets d'un carré ...

[sue]

bonjour,

soit M d'aff et M' d'aff
je cherche les affixes de N et N' t.q MNM'N' est un carré de diamétre [MM'] .
---
j'ai introduit donc la rotation donc on a : et et f l'aplicattion qui à chaque point M associe M' t.q :
soit z1 et z2 les affixes respectives de N et N' , on a donc :
z1 =
z2 =

est-ce juste ? :hein:

[sue]

pourriez-vous comfirmer ou infirmer svp ?

[Elsa_toup]

Ca a l'air bon, mais j'avoue trouver ça un brin compliqué.
De plus, j'ai 2 petites questions :
1. qu'est-ce qu'un carré de diamètre [MM'] ?
2. que signifie le -1 dans r(-1,pi/2) ?

[sue]

oh désolée :girl2: je voulais dire ''le carré de digonale [MM'] , j'étudie pas les maths en français alors ça m'arrive parfois de confondre les termes .
pour l'autre question en fait c'est : r(c(-1) , pi/2) i.e la rotaion de centre c(-1) et d'angle pi/2 .

Ca a l'air bon, mais j'avoue trouver ça un brin compliqué.

y a plus simple stp ?

[Elsa_toup]

Non, je réfléchis, mais en fait c'est aussi long de passer par les coordonnées des vecteurs, ou encore par la symétrie de centre le milieu de [MM'].

Je retire donc mon commentaire. Tu as très bien fait ! :lol4:

[sue]

merci pour la comfirmation :happy3:

en fait j'ai une autre question si vous pouvez m'aider ..
soit l'équation (E) : admettant deux solutions z et z' et .
je cherche à déterminer t.q :
1) z et z' sont des réels
2) z et z' sont des imaginaires purs .

en fait pour le premier cas je crois qu'il faut utiliser le fait que \Delta est est un réel strict. positif i.e , n'est-ce pas ?

[Elsa_toup]

Oui c'est cela. sera en effet >0, donc il y a deux solutions distinctes z et z'.
Elles sont données par une formule qu'il faut expliciter.

[sue]

je comprend pas une chose :hein:
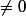
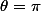
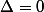
delta doit etre or on a donc pour que les racines soient réels il faut que ou donc soit z=z' :hein:

[Elsa_toup]

Je me trompe sûrement (tu as l'air meilleure que moi en Maths ... ), mais comment calcules-tu ? Parce que je ne trouve pas la même chose ...

[sue]

en fait tu as raison je me suis trompée c'est : non ?

[Elsa_toup]

Oui, tout à fait d'accord.

[sue]

je délire là mais si alors il faut que or pi/2 n'appartient pas à cet intervalle .
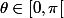
et si alors il faut que = -pi/2 et meme probleme :hein:

[Elsa_toup]

Pourquoi donc?
est positif, ça c'est sûr.
Donc tout va bien...

[sue]

si Delta est positif alors il ya 2 possibilités :
1)soit et
2)soit et
donc
1) et = -pi/2 --- absurde il me semble .
2) et --- absurde . :hein:

je comprend pas

[sue]

est positif, ça c'est sûr.
Donc tout va bien...

pouvez-vous m'expliquer svp ?

[Elsa_toup]

Non, en fait rien ne va.... :cry: (lol)
Je n'arrive pas à remettre le doigt sur mes souvenirs de lycée.
Dans quel cas les racines d'un polynômes à valeurs complexes sont-elles réelles ?

Parce que là on a une racine de complexe... Je ne suis pas ravie ...

[sue]

Dans quel cas les racines d'un polynômes à valeurs complexes sont-elles réelles ?

la condition de delta réel positif ne suffit pas ?

[Elsa_toup]

Ah c'est possible...
Mais cela m'étonne, car supposons réel, disons même =1.
Les racines seront et , qui ne sont pas forcément réelles ....

[sue]

re,

Bon je passe à la 2ème partie de mon exo :
soit
posons Z= z-p et Z'= z'-p
1) calculer Z+Z' et Z.Z' en fonction de p .(c bon j'ai fait )
2) en déduire l'argument et le module de Z et Z' ; discuter selon

je trouve et

2) on a Z et Z' sont solutions de l'équation : aprés je résous l'équation , mais je vois pas quels cas de \theta je dois discuter :hein:

[sue]

bonjour,

bon j'ai peut etre une idée pour la question précédente :

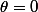
alors si z et z' sont deux racines réels , biensur que z+z' est un réel or on a donc donc ou

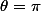
idem pour le 2ème cas de z et z' imaginaires purs : donc ou