J'ai l'impression que tu as trouvé l'astuce qu'il fallait ! :we:
Bravo à toi ! :++:
Affixes des sommets d'un carré ...
25 messages
- Page 2 sur 2 - 1, 2
sue a écrit:j'ai introduit donc la rotation
Je n'ai pas encore tout lu...mais je m'arrête tout de suite ! Pour quelle raison veux-tu introduire cette rotation ? Tu veux bien tourner autour du milieu de MM' n'est-ce pas ? Si oui, je te signale que le point -1 n'est pas le milieu de MM' !
M :
M' :
Le milieu de MM' a donc pour affixe :
Donc, il est clair que l'application f à laquelle tu fais référence dans ton tout premier post, n'est pas la bonne !
Je n'ai pas lu ce fil jusqu'au bout, mais ne serait-ce pas une cause de tes problèmes ultérieurs ????
sue a écrit:merci pour la comfirmation :happy3:
en fait j'ai une autre question si vous pouvez m'aider ..
soit l'équation (E) :admettant deux solutions z et z' et
.
je cherche à déterminert.q :
1) z et z' sont des réels
2) z et z' sont des imaginaires purs .
en fait pour le premier cas je crois qu'il faut utiliser le fait que \Delta est est un réel strict. positif i.e, n'est-ce pas ?
NON ! Les racines d'un trinôme ax²+bx+c sont données par :
Même si
merci Quidam d'avoir regardé mon problème :we:
désolée je vois pas de contradiction entre mon résultat et le votre , on pourrait bien écrire :
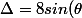(-\sin(\theta)+i\cos(\theta) = 8sin(\theta) e^{i(\frac{\pi}{2} + \theta)} = 8isin(\theta) e^{i\theta}) non?
non?
sinon que dites vous de la dernière conclusion :
est-ce suffisant ?
sinon merci de m'avoir corrigé à propos du centre de la rotation .
Quidam a écrit:Ben non !
désolée je vois pas de contradiction entre mon résultat et le votre , on pourrait bien écrire :
sinon que dites vous de la dernière conclusion :
sue a écrit:alors si z et z' sont deux racines réels , biensur que z+z' est un réel or on adonc
donc
ou
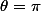
idem pour le 2ème cas de z et z' imaginaires purs :donc
ou
est-ce suffisant ?
sinon merci de m'avoir corrigé à propos du centre de la rotation .
25 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
