Affixe d'un vecteur

[Benoît]

Bonjour,
Il me reste deux exercices sur mon DM de Maths que je ne comprends pas, si quelqu'un peut m'expliquer, ça pourra beaucoup m'aider.

Exercice 1 :

est la translation de vecteur d'affixe
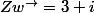
On pose

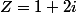
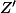
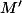
Calculer l'affixe du point image de par la translation

Exercice 2 :

est la rotation de centre O et d'angle
On pose

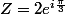
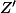
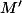
Calculer l'affixe du point image de par la rotation

Merci d'avance !

[annick]

Bonjour,
pour une translation, on sait que vecteur MM'= vecteur W.

Comment traduis-tu cela sous forme complexe ?

[Black Jack]

Cela aurait quand même été mieux, si l'énoncé avait précisé que le point M avait Z pour affixe.

Cela va peut être sans dire ... mais cela va encore mieux en le disant.

[Benoît]

Bonjour,
pour une translation, on sait que vecteur MM'= vecteur W.

Comment traduis-tu cela sous forme complexe ?

Sous forme complexe, c'est a dire sous forme algébrique / exponentielle ?

[annick]

Pour la translation, la dorme algébrique est la plus évidente.

[Benoît]

Pour la translation, la dorme algébrique est la plus évidente.

Et je dois faire comment pour l'avoir ?

[annick]

Bon, je ne réécris pas "vecteur" à chaque fois, mais je vais parler en vecteurs.

Comme je te le disais, je suppose que tu as vu que la translation correspond à MM'=W, soit :

OM'-OM=W

Or, avec les complexes, OM' correspond à Z' et OM à Z.

Donc, traduction complexe : Z'=Z+W et ainsi tu obtiendras l'affixe de M'.

(Et tu pourras vérifier sur une figure que ta réponse est juste.)

[Benoît]

Si je comprends bien, par exemple pour l'exercice 1 je dois faire :

Z' = (1+2 i) + (3 + i)

C'est ca ?

[annick]

Oui, c'est cela, mais comprends-tu pourquoi ? Vois-tu bien ce qu'est une translation. Vois-tu bien les correspondances géométriques, vectorielles avec les complexes ?

[Benoît]

Oui, c'est cela, mais comprends-tu pourquoi ? Vois-tu bien ce qu'est une translation. Vois-tu bien les correspondances géométriques, vectorielles avec les complexes ?

Difficilement

[annick]

Essaye de bien reprendre ton cours et de le regarder en fonction de ce que tu as vu dans cet exercice. Je suis sûre que cela devrait t'éclairer. Allez, courage, avec de la persévérance tu vas y arriver.