Addition de fraction

[Mehdi.H]

Bonsoir,

Je dois trouver en additionnant une suite de 5 fractions et de 10 fractions trouver les dénominateurs tous différents pour que le résultat soit toujours égal à 1. Et dire comment vous l'avez trouvé et pourquoi cela fonctionne.






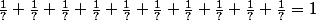
Je n'ai pas compris.

Merci

[Vat02]

Bonsoir,

Je dois trouver en additionnant une suite de 5 fractions et de 10 fractions trouver les dénominateurs tous différents pour que le résultat soit toujours égal à 1. Et dire comment vous l'avez trouvé et pourquoi cela fonctionne.






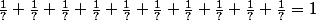
Je n'ai pas compris.

Merci

Tu remplaces simplement le ? par x (pour l'habitude)

Tu as à 5 reprises 1/x ce qui revient à 5/x = 1 d'où x = ....

Même chose pour le 1/? (ou 1/x) à 10 reprises

[Mehdi.H]

Tu remplaces simplement le ? par x (pour l'habitude)

Tu as à 5 reprises 1/x ce qui revient à 5/x = 1 d'où x = ....

Même chose pour le 1/? (ou 1/x) à 10 reprises

Je n'ai pas bien compris comment trouver les dénominateurs, est ce que vous pouvez me faire un exemple avec celui à 5 reprises svp et me dire le calcul que vous faites pour trouver le dénominateur suivant.
Merci

[annick]

Bonjour,

Double post !!! http://www.maths-forum.com/showthread.php?goto=newpost&t=137034

Ce n'est jamais très respectueux pour les personnes qui ont commencé à te répondre sur l'autre post !!!

[Kikoo <3 Bieber]

Tu remplaces simplement le ? par x (pour l'habitude)

Tu as à 5 reprises 1/x ce qui revient à 5/x = 1 d'où x = ....

Même chose pour le 1/? (ou 1/x) à 10 reprises

Salut Vat02,

Justement, le but de l'exo est de déterminer 5 fractions distinctes de la forme 1/x.
Comme nous avions commencé par le dire dans l'autre post, il s'agit de déterminer d'abord une fraction strictement plus petite que 1 et de la forme 1/n, n entier. Nous avons beaucoup de choix. Et par la densité de Q et I dans R, cela nous permet de trouver une flopée de fractions qui conviennent, aussi petites soient-elles.

[Vat02]

Salut Vat02,

Justement, le but de l'exo est de déterminer 5 fractions distinctes de la forme 1/x.
Comme nous avions commencé par le dire dans l'autre post, il s'agit de déterminer d'abord une fraction strictement plus petite que 1 et de la forme 1/n, n entier. Nous avons beaucoup de choix. Et par la densité de Q et I dans R, cela nous permet de trouver une flopée de fractions qui conviennent, aussi petites soient-elles.

Arf désolé, je m'y reprendrai à 2 fois en lisant l'énoncé dorénavant.