Bonjour, je suis en seconde et j'aimeais bien que vous m'expliquiez comment résoudre une equation de ce type:
3x²-2x-7=0
j'ai essayé longtemps, j'ai aussi demandé à des amis qui m'ont expliqué un truc avec "delta"... je n'ai pas encore vu "delta" et j'aimerais bien savoir comment résoudre cette equation. SVP, aidez moi !
Merci
2nde: equations, probleme...
7 messages
- Page 1 sur 1
Je veux bien t'expliquer mais l'exemple que tu as choisi n'est pas des plus simples , si tu le permets , j'en choisi un autre :  . L'idée est de reconnaitre le début d'un produit remarquable :
. L'idée est de reconnaitre le début d'un produit remarquable :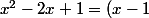^2) . On l'utilise en corrigeant :
. On l'utilise en corrigeant :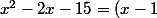^2-16) . On reconnait alors un nouveau produit remarquable
. On reconnait alors un nouveau produit remarquable ^2-16=(x-1)^2-4^2=(x-5)(x+3)) et on a les deux solutions de l'équation
et on a les deux solutions de l'équation  , x = 5 et x=-3 .
, x = 5 et x=-3 .
Imod
Imod
D'identité remarquable, on en aperçoit quand même deux petis bouts : x²...1.hippoleg a écrit:x²-x-1=0 je suis coincé :mur:
Alors pourquoi ne pas tenter ta chance avec (x+1)² ? :zen:
Quand tu auras trouver le terme correcteur
qu'il faut "ajouter" à (x+1)² pour obtenir x²-x-1,
tu verras - peut-être - la chance te sourire
sous la forme d'un facteur bienvenu... :id:
c pi a écrit:D'identité remarquable, on en aperçoit quand même deux petis bouts : x²...1.
Alors pourquoi ne pas tenter ta chance avec (x+1)² ? :zen:
Quand tu auras trouver le terme correcteur
qu'il faut "ajouter" à (x+1)² pour obtenir x²-x-1,
tu verras - peut-être - la chance te sourire
sous la forme d'un facteur bienvenu... :id:
ttt, ttt !
Moi je verrais plutôt deux autres petits bouts : x²-x..., ce qui mène à
Je suis d'accord avec la fin :
Alors pourquoi ne pas tenter ta chance avec
Quand tu auras trouvé le terme correcteur
qu'il faut "ajouter" à
tu verras - peut-être - la chance te sourire
sous la forme d'un facteur bienvenu... :id:
Le facteur sonne toujours deux fois :
d'abord un coup, puis un demi-coup de moins.
Alors on ouvre dès le premier coup (avant l'effraction)
ou un peu après si l'on ne craint point les fractions. :zen:
Bien vu Quidam ! :salut:
Mais avec les fractions,
le facteur apporte une bonne nouvelle : la solution est juste ! :++:
Alors que sans,
le facteur bienvenu ne m'était apparu qu'en rêve :
quand un nombre dort, il ne faut pas en coucher un autre.
Où avais-je la tête ! :marteau:
d'abord un coup, puis un demi-coup de moins.
Alors on ouvre dès le premier coup (avant l'effraction)
ou un peu après si l'on ne craint point les fractions. :zen:
Bien vu Quidam ! :salut:
Mais avec les fractions,
le facteur apporte une bonne nouvelle : la solution est juste ! :++:
Alors que sans,
le facteur bienvenu ne m'était apparu qu'en rêve :
quand un nombre dort, il ne faut pas en coucher un autre.
Où avais-je la tête ! :marteau:
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
