2èm exo barycentre
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Anna_05
- Membre Naturel
- Messages: 88
- Enregistré le: 30 Oct 2009, 10:26
-
 par Anna_05 » 21 Jan 2011, 21:10
par Anna_05 » 21 Jan 2011, 21:10
Bonjour, j'ai encore une fois un exercice sur les barycentres j'ai fait l'exercice en entier sauf que j'ai du mal à justifier une question: voici le sujet
ABC est un triangle équilatéral, AB=6cm
1-Construire le barycentre G des points pondérés (A,1)(B,-1)(C,2)
2-Déterminer l'ensemble E des points M du plan tel que ||MA-MB+2MC||=AB (vecteur)
Donc c'est le cercle de centre G et de rayon 3 cm. Puis il me demande de montrer que le point C appartient à cet ensemble. J'essaye de remplacer M par C mais j'obtiens à la fin ||CG||=||0.5CA-05CB||(vecteur) comment je fait maintenant pour montrer que c'est égal à 3 ?
Merci,
-
geegee
- Membre Rationnel
- Messages: 799
- Enregistré le: 11 Mai 2008, 13:17
-
 par geegee » 21 Jan 2011, 21:21
par geegee » 21 Jan 2011, 21:21
Bonjour,
On remplace M par C et on obtient:
||CA-CB+2CC||= ||CA-CB|| = ||BA||=AB donc C appartien a ce cercle.
-
bmiras
- Membre Naturel
- Messages: 67
- Enregistré le: 18 Jan 2011, 00:51
-
 par bmiras » 21 Jan 2011, 21:23
par bmiras » 21 Jan 2011, 21:23
Anna_05 a écrit:Bonjour, j'ai encore une fois un exercice sur les barycentres j'ai fait l'exercice en entier sauf que j'ai du mal à justifier une question: voici le sujet
ABC est un triangle équilatéral, AB=6cm
1-Construire le barycentre G des points pondérés (A,1)(B,-1)(C,2)
2-Déterminer l'ensemble E des points M du plan tel que ||MA-MB+2MC||=AB (vecteur)
Donc c'est le cercle de centre G et de rayon 3 cm. Puis il me demande de montrer que le point C appartient à cet ensemble. J'essaye de remplacer M par C mais j'obtiens à la fin ||CG||=||0.5CA-05CB||(vecteur) comment je fait maintenant pour montrer que c'est égal à 3 ?
Merci,
Juste pour voir, tu remplace M par C dans quelle expression?
-
Anna_05
- Membre Naturel
- Messages: 88
- Enregistré le: 30 Oct 2009, 10:26
-
 par Anna_05 » 21 Jan 2011, 21:27
par Anna_05 » 21 Jan 2011, 21:27
Eh bien je l'ai remplacer dans l'expression de la question numéro 2 et je voudrais vraiment savoir pourquoi cela n'a pas marcher, merci
-
bmiras
- Membre Naturel
- Messages: 67
- Enregistré le: 18 Jan 2011, 00:51
-
 par bmiras » 21 Jan 2011, 21:28
par bmiras » 21 Jan 2011, 21:28
Anna_05 a écrit:Eh bien je l'ai remplacer dans l'expression de la question numéro 2 et je voudrais vraiment savoir pourquoi cela n'a pas marcher, merci
Tu envoies le détail de ta recherche suite au remplacement?
-
Anna_05
- Membre Naturel
- Messages: 88
- Enregistré le: 30 Oct 2009, 10:26
-
 par Anna_05 » 21 Jan 2011, 21:29
par Anna_05 » 21 Jan 2011, 21:29
Non en faite je suis parti su le fait que alpha MA+betaMB+gama MC= alpha+beta+gama CG
donc CG=1/2 CA-1/2CB ce qui le donne 0.5 CA-0.5 CB
-
bmiras
- Membre Naturel
- Messages: 67
- Enregistré le: 18 Jan 2011, 00:51
-
 par bmiras » 21 Jan 2011, 21:35
par bmiras » 21 Jan 2011, 21:35
Anna_05 a écrit:Non en faite je suis parti su le fait que alpha MA+betaMB+gama MC= alpha+beta+gama CG
donc CG=1/2 CA-1/2CB ce qui le donne 0.5 CA-0.5 CB
Ca sort d'où ton alpha MA+betaMB+gama MC= alpha+beta+gama CG?
-
Anna_05
- Membre Naturel
- Messages: 88
- Enregistré le: 30 Oct 2009, 10:26
-
 par Anna_05 » 21 Jan 2011, 21:38
par Anna_05 » 21 Jan 2011, 21:38
Eh bien c'est une propriété du cours
-
bmiras
- Membre Naturel
- Messages: 67
- Enregistré le: 18 Jan 2011, 00:51
-
 par bmiras » 21 Jan 2011, 21:40
par bmiras » 21 Jan 2011, 21:40
Anna_05 a écrit:Eh bien c'est une propriété du cours
Ce serait pas plutôt:
alphaMA+betaMB+gamma MC= (alpha+beta+gamma) MG
la propriété du cours?
-
Anna_05
- Membre Naturel
- Messages: 88
- Enregistré le: 30 Oct 2009, 10:26
-
 par Anna_05 » 21 Jan 2011, 21:42
par Anna_05 » 21 Jan 2011, 21:42
Euh oui effectivement je m'excuse de l'erreur, cela doit être la fatigue...
-
bmiras
- Membre Naturel
- Messages: 67
- Enregistré le: 18 Jan 2011, 00:51
-
 par bmiras » 21 Jan 2011, 21:44
par bmiras » 21 Jan 2011, 21:44
Anna_05 a écrit:Euh oui effectivement je m'excuse de l'erreur, cela doit être la fatigue...
Tu tentes à nouveau un truc alors? (on croise les doigts) :we:
-
Anna_05
- Membre Naturel
- Messages: 88
- Enregistré le: 30 Oct 2009, 10:26
-
 par Anna_05 » 21 Jan 2011, 21:50
par Anna_05 » 21 Jan 2011, 21:50
Oui merci j'essaye
-
Anna_05
- Membre Naturel
- Messages: 88
- Enregistré le: 30 Oct 2009, 10:26
-
 par Anna_05 » 21 Jan 2011, 21:58
par Anna_05 » 21 Jan 2011, 21:58
Jespère que c'est juste maintenant:
MG=0.5MA-0.5MB+MC
MG=MC
||MG||=||MC||
On sait que le cercle à un rayon de 3 cm donc MC=3 cm, donc C appartient au cercle de centre G et de rayon 3
-
bmiras
- Membre Naturel
- Messages: 67
- Enregistré le: 18 Jan 2011, 00:51
-
 par bmiras » 21 Jan 2011, 22:03
par bmiras » 21 Jan 2011, 22:03
Anna_05 a écrit:Jespère que c'est juste maintenant:
MG=0.5MA-0.5MB+MC
MG=MC
||MG||=||MC||
On sait que le cercle à un rayon de 3 cm donc MC=3 cm, donc C appartient au cercle de centre G et de rayon 3
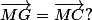
-
Anna_05
- Membre Naturel
- Messages: 88
- Enregistré le: 30 Oct 2009, 10:26
-
 par Anna_05 » 21 Jan 2011, 22:06
par Anna_05 » 21 Jan 2011, 22:06
Je vais vraiment m'endormir, je vais essayer encore une fois ...
-
Anna_05
- Membre Naturel
- Messages: 88
- Enregistré le: 30 Oct 2009, 10:26
-
 par Anna_05 » 21 Jan 2011, 22:09
par Anna_05 » 21 Jan 2011, 22:09
Mais si je mais les ormes par la suite, car notre but est de démontrer la disctance cela me donnerait:
||MG||=||0.5MA-0.5MB+MC||
Nous sommes dans un triangle équilatéral de 6 cm donc
||MG||=3-3+MC||
On connait la distance MG c'est le rayon donc 3 cm
3=MG
-
bmiras
- Membre Naturel
- Messages: 67
- Enregistré le: 18 Jan 2011, 00:51
-
 par bmiras » 21 Jan 2011, 22:14
par bmiras » 21 Jan 2011, 22:14
Anna_05 a écrit:Mais si je mais les ormes par la suite, car notre but est de démontrer la disctance cela me donnerait:
||MG||=||0.5MA-0.5MB+MC||
Nous sommes dans un triangle équilatéral de 6 cm donc
||MG||=3-3+MC||
On connait la distance MG c'est le rayon donc 3 cm
3=MG
Donc M est sur le cercle?
Ce n'est pas comme cela qu'on manipule les normes d'ailleurs...
Il faut te poser cinq secondes et te demander ce que veux dire: C appartient à E (tel qu'est défini E)...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
