Bonjour, je vous poste le 2e devoir de maths de 2nde de mon frère pour vous entrainer si besoin est, l'usage de la calculatrice est censé être interdit et la durée du devoir est de deux heures pour information ^^. Si certain désire une correction, je prendrai soin de vous la détailler. Il n'y a, selon moi, que les deux derniers exercices qui méritent réflexion pour un seconde. Bon travail.
Exercice 1a) Soit
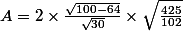
; écrire

sous la forme
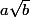
, avec

entier le plus petit possible.
b) Soit
^2\times (8^2)^{-3}}{-32^{-2}})
; en utilisant des puissances de

, calculer

.
Exercice 2Résoudre dans

les équations suivantes :
1°)
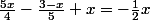
;
2°)
 - x(x-3)= - (x^2+6))
;
3°)
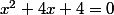
;
4°)

;
5°)
(x-4)=(x+2)(2x-3))
;
6°)
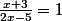
;
7°)
(4-12x+9x^2)}{3x-2}=0)
;
8°)
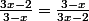
;
9°)
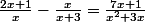
.

On pose
=(4x-5)^2-(3+x)(5-4x)-16x^2+25)
.
1°) Développer et réduire f(x), on montrera que f(x)=4x^2-33x+35.
2°) Factoriser f(x).
3°) Calculer
)
et
)
.
4°) Résoudre les équations : f(x)=0 puis f(x)=3(12-11x).
Exercice 4Soit

un entier naturel et

le nombre défini par
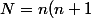(n+2)(n+3)+1)
.
1°) Calculer

pour

, pour

et pour

.
Vérifier dans chacun des cas,

est un carré parfait, c'est-à-dire le carré d'un entier naturel.
2°) Le but de cette question est donc de démontrer que pour tout entier naturel

,

est un carré parfait.
a) Montrer que :
(n+2)=n(n+3)+2)
.
b) On pose :
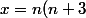)
. Exprimer

en fonction de

seulement et en déduire que

est bien un carré parfait.
3°) Déduire de la question précédente de quel nombre
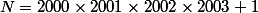
est le carré.
Exercice 5Le réel
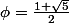
est appelé nombre d'or.

est une lettre grecque nommée "phi".
1°) Calculer

puis
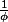
sans radical au dénominateur.
2°) En déduire que :
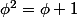
.
3°) En déduire
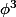
en fonction de

sous la forme

, où

et

sont deux entiers à déterminer.
4°) En déduire
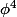
et
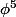
en fonction de

. Donner l'expression numérique de
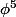
.
