Dm 1es
24 messages
- Page 1 sur 2 - 1, 2
Dm 1es
Bonjour,
Je voulais savoir si vous pouviez m'aider sur plusieurs points de mon DM. Sa serait très gentil de votre part.
Je vous le recopie et vous explique se que je n'ai pas compris.
Soit f la fonction définie par f(x) = (10x)/(x²+1) de représentation graphique Cf.
1) Quel est le domaine de définition Df de f.
Là j'ai un petit problème. En cherchant j'ai trouvé x²+1 = 0 donc x² = -1 seulement c'est impossible et je ne vois pas comment sa se fait.
2) Calculer f(1), f(-1), f(3) et f(-3). Là je pense pas qu'il y de problème j'ai trouvé 5, -5, 3 et -3.
3) Pourver que pour tout nombre réel x f(-x) = -f(x).
Là je ne sais pas comment le prouver mais avec un exemple on voit que sa donne sa.
4) Vérifier que f '(x) = (10(1-x)(1+x))/(x²+1)²
Là je ne sais pas developper la première ligne. Faut-il d'abord developer 10(1-x) ou (1-x)(1+x) ??
5)Etablir le tableau des signes de l'expression f' (x). On distinguera trois intervalles. Je n'ai jamais très bien compris cette histoire de tableau de signes mais c'est trouvé le signe de 10(1-x)(1+x) puis celui de (x²+1)² pour en déduire celui de l'expression entière ??
6) En déduire le tabeau de variation. Bon ça je pense qu'il n'y a pas de problème.
7) Construire la courbe Cf sur l'intervalle [ -8; 8 ].
Là aucun problème.
8)Comparer f(3) et f(1/3) et comparer f(2) et (1/2). Là pas de problème.
Plus généralement prouver que pour tout nombre réel x différent de 0, f(1/x) = f(x). Làje ne vois pas trop comment faire.
9)Trouver l'équation de la tagente à Cf au point A d'abscisse 2 de Cf.
Là il faut trouver y= ax+b ???
10) Trouver par calcul les solutions de l'équation f(x)=5.
Pourriez vous m'aider ??
Merci d'avance.
Je voulais savoir si vous pouviez m'aider sur plusieurs points de mon DM. Sa serait très gentil de votre part.
Je vous le recopie et vous explique se que je n'ai pas compris.
Soit f la fonction définie par f(x) = (10x)/(x²+1) de représentation graphique Cf.
1) Quel est le domaine de définition Df de f.
Là j'ai un petit problème. En cherchant j'ai trouvé x²+1 = 0 donc x² = -1 seulement c'est impossible et je ne vois pas comment sa se fait.
2) Calculer f(1), f(-1), f(3) et f(-3). Là je pense pas qu'il y de problème j'ai trouvé 5, -5, 3 et -3.
3) Pourver que pour tout nombre réel x f(-x) = -f(x).
Là je ne sais pas comment le prouver mais avec un exemple on voit que sa donne sa.
4) Vérifier que f '(x) = (10(1-x)(1+x))/(x²+1)²
Là je ne sais pas developper la première ligne. Faut-il d'abord developer 10(1-x) ou (1-x)(1+x) ??
5)Etablir le tableau des signes de l'expression f' (x). On distinguera trois intervalles. Je n'ai jamais très bien compris cette histoire de tableau de signes mais c'est trouvé le signe de 10(1-x)(1+x) puis celui de (x²+1)² pour en déduire celui de l'expression entière ??
6) En déduire le tabeau de variation. Bon ça je pense qu'il n'y a pas de problème.
7) Construire la courbe Cf sur l'intervalle [ -8; 8 ].
Là aucun problème.
8)Comparer f(3) et f(1/3) et comparer f(2) et (1/2). Là pas de problème.
Plus généralement prouver que pour tout nombre réel x différent de 0, f(1/x) = f(x). Làje ne vois pas trop comment faire.
9)Trouver l'équation de la tagente à Cf au point A d'abscisse 2 de Cf.
Là il faut trouver y= ax+b ???
10) Trouver par calcul les solutions de l'équation f(x)=5.
Pourriez vous m'aider ??
Merci d'avance.
salut,
oui effectivement il faut que x²+1#0 pour que ta fonction soit definie or un carré plus un nombre positif as-ton avis est-ce que ça s'annule sur R?...
) Quel est le domaine de définition Df de f.
Là j'ai un petit problème. En cherchant j'ai trouvé x²+1 = 0 donc x² = -1 seulement c'est impossible et je ne vois pas comment sa se fait.
oui effectivement il faut que x²+1#0 pour que ta fonction soit definie or un carré plus un nombre positif as-ton avis est-ce que ça s'annule sur R?...
2) Calculer f(1), f(-1), f(3) et f(-3). Là je pense pas qu'il y de problème j'ai trouvé 5, -5, 3 et -3.
non il n'y a pas de probleme c'est bon
3) Pourver que pour tout nombre réel x f(-x) = -f(x).
Là je ne sais pas comment le prouver mais avec un exemple on voit que sa donne sa.
il suffit que tu remplace x par -x dans l'expression de f
ce que je trouve bizarre c'est qu'il ne demande de rien pour le fait que f(-x)=-f(x) (sinon ça veut dire que ta fonction est impaire donc qu'elle admet le point O comme centre de symetrie)
as-tu calculé ta dérivée?
4) Vérifier que f '(x) = (10(1-x)(1+x))/(x²+1)²
Là je ne sais pas developper la première ligne. Faut-il d'abord developer 10(1-x) ou (1-x)(1+x) ??
as-tu calculé ta dérivée?
on y va pour le calcul
}=\frac{(10x)'(x^2+1)-10x(x^2+1)'}{(x^2+1)^2}=\frac{10(x^2+1)-10x(2x)}{(x^2+1)^2}=\frac{10x^2+10x-20x^2}{(x^2+1)^2}=\frac{-10x^2+10x}{(x^2+1)^2})
je sais pas comment tu as fait pour trouver le 20x?
apres il suffit de factoriser le numerateur donc
}=\frac{10(-x^2+1}{(x^2+1)^2}=\frac{10(1-x^2)}{(x^2+1)^2}=\frac{10(1-x)(1+x)}{(x^2+1)^2})
dans 1-x² on reconnait a²-b²=(a-b)(a+b)
f'(x) sera du signe de (1-x)(1+x) car sur R 10/(x²+1)²>0
donc il faut regarder le signe de la derivée sur ]-inf,-1] sur [-1,1] et sur [1,+inf[
d'où un petit tableau de signe
je sais pas comment tu as fait pour trouver le 20x?
apres il suffit de factoriser le numerateur donc
dans 1-x² on reconnait a²-b²=(a-b)(a+b)
5)Etablir le tableau des signes de l'expression f' (x). On distinguera trois intervalles. Je n'ai jamais très bien compris cette histoire de tableau de signes mais c'est trouvé le signe de 10(1-x)(1+x) puis celui de (x²+1)² pour en déduire celui de l'expression entière ??
f'(x) sera du signe de (1-x)(1+x) car sur R 10/(x²+1)²>0
donc il faut regarder le signe de la derivée sur ]-inf,-1] sur [-1,1] et sur [1,+inf[
d'où un petit tableau de signe
bon si tu as compris le truc on passe à la suite
8) il suffit de remlacer x par 1/x dans l'expression de f
9) rappel:
equation de la tangente au poit d'abscisse xo est donnée par
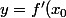(x-x_0)+f(x_0))
donc ici x0=2 donc
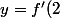(x-2)+f(2)) tu connais f(x) et f'(x) donc pas de probleme
tu connais f(x) et f'(x) donc pas de probleme
10)
f(x)=5
10x/(x²+1)=5
10x=5(x²+1)
10x=5x²+5
5x²-10x+5=0
5(x²-2x+1)=0
...
8)Comparer f(3) et f(1/3) et comparer f(2) et (1/2). Là pas de problème.
Plus généralement prouver que pour tout nombre réel x différent de 0, f(1/x) = f(x). Làje ne vois pas trop comment faire.
9)Trouver l'équation de la tagente à Cf au point A d'abscisse 2 de Cf.
Là il faut trouver y= ax+b ???
10) Trouver par calcul les solutions de l'équation f(x)=5.
8) il suffit de remlacer x par 1/x dans l'expression de f
9) rappel:
equation de la tangente au poit d'abscisse xo est donnée par
donc ici x0=2 donc
10)
f(x)=5
10x/(x²+1)=5
10x=5(x²+1)
10x=5x²+5
5x²-10x+5=0
5(x²-2x+1)=0
...
24 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 71 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
