Dm 1ere ES
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
emiliey
- Membre Relatif
- Messages: 142
- Enregistré le: 07 Mar 2012, 11:32
-
 par emiliey » 07 Mar 2012, 16:46
par emiliey » 07 Mar 2012, 16:46
Sylviel a écrit:Certes, sauf que tu n'as pas répondu à ma question : comment faire pour montrer qu'une suite est arithmétique ?
If faut montrer que Un+1 = Un + r (avec r qui ne dépends pas de n !!!)
Et pour montrer qu'elle est géométrique ?
Mais je l'ai dit avant avec:
Alors, pour savoir si elle est arithmétique, on fait Un+1 = Un+r
On doit passer d'un terme à l'autre en ajoutant toujours le même nombre qui est la raison r.
Et pour savoir si elle est géométrique, on utilise cette formule : Un+1 = Un*q
On doit passer d'un terme à l'autre en multipliant toujours par le meme nombre..
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 07 Mar 2012, 16:48
par Sylviel » 07 Mar 2012, 16:48
Ok, j'avais pas vu qu'il y avait 3 messages.
Bon et que vaut Vn+1 (la définition) ? Vn+1 = ...
Ensuite utilise la définition de Un+1
Puis essaie de "faire apparaître" du Vn.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
emiliey
- Membre Relatif
- Messages: 142
- Enregistré le: 07 Mar 2012, 11:32
-
 par emiliey » 07 Mar 2012, 16:51
par emiliey » 07 Mar 2012, 16:51
Sylviel a écrit:Ok, j'avais pas vu qu'il y avait 3 messages.
Bon et que vaut Vn+1 (la définition) ? Vn+1 = ...
Ensuite utilise la définition de Un+1
Puis essaie de "faire apparaître" du Vn.
Désolée j'ai écris plusieurs fois....
Mais on ne me donne pas ce que vaut Vn+1 dans l'énoncé de l'exercice :/
Je dois trouver moi même? Mais comment?

(J'y arrive vraiment pas avec ces suites...)
-
emiliey
- Membre Relatif
- Messages: 142
- Enregistré le: 07 Mar 2012, 11:32
-
 par emiliey » 07 Mar 2012, 17:22
par emiliey » 07 Mar 2012, 17:22
Aidez-moi svp :'(
Je suis vraiment bloquée..
 par MathsAdvices » 07 Mar 2012, 17:30
par MathsAdvices » 07 Mar 2012, 17:30
emiliey a écrit:Bonjour à tous!
Je suis en 1ère ES
Je suis nouvelle sur ce site..
Le problème que j'ai c'est que j'ai un DM de math et il y a un exercice sur les suites que je n'arrive pas à le faire entièrement :/ à partir de la question 3 je bloque.. donc j'aimerai bien avoir un peu d'aide de votre part Svp :$
Voici l'exercice:
on considère la suite Un pour tout n appartenant à N : U0= 2 et Un+1= 2/3Un+1 , pour n appartient à N
1) Calculer u1, u2, u3
2) la suite (Un) est-elle arithmétique ? géométrique?
(a partir de là je n'y arrive plus .. )
3) on définit la suite (Vn) par Vn=Un-3 pour tout n appartient à N
a. calculer V0, V1, V2
b. Déterminer la nature de la suite (Vn)
c. En déduire l'expression de Vn en fonction de n
4) a.Exprimer Un en fonction de Vn, puis en fonction de n
b. Calculer U8
Aidez moi svp :'(
Je vous remercie d'avance, en attendant une réponse assez rapidement de votre part!
Emilie.Y
Voici un cours sur les suites :
http://mathsadvices.wordpress.com/2012/03/06/les-suites-numeriques-les-bases/Si tu as des questions, je pourrai t'aider à y voir plus clair
-
emiliey
- Membre Relatif
- Messages: 142
- Enregistré le: 07 Mar 2012, 11:32
-
 par emiliey » 07 Mar 2012, 17:32
par emiliey » 07 Mar 2012, 17:32
Merci de votre attention

Je vais y jeter un coup d'oeil au site que vous m'avez conseillé..
Et je reviens vers vous si j'ai encore des soucis..

-
emiliey
- Membre Relatif
- Messages: 142
- Enregistré le: 07 Mar 2012, 11:32
-
 par emiliey » 07 Mar 2012, 17:38
par emiliey » 07 Mar 2012, 17:38
Le cours est parfait! Comme celui que mon professeur de maths nous a donné

Maintenant le problème que j'ai c'est dans l'exercice.. Je n'arrive pas à partir de la question 3

Sylviel m'a aidé comme vous pouvez le voir, mais je n'ai toujours pas réussi à répondre aux questions 3) a,b,c et 4 a,b ....
-
emiliey
- Membre Relatif
- Messages: 142
- Enregistré le: 07 Mar 2012, 11:32
-
 par emiliey » 07 Mar 2012, 19:33
par emiliey » 07 Mar 2012, 19:33
Il n'y a personne pour me donner un peu d'aide par ici svp? :(
-
globule rouge
- Membre Irrationnel
- Messages: 1011
- Enregistré le: 16 Fév 2012, 16:38
-
 par globule rouge » 07 Mar 2012, 20:44
par globule rouge » 07 Mar 2012, 20:44
Hello =)
Tu sais bien que
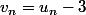
Ainsi,
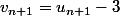
Or il te semble, d'après les résultats du 3)b), que cette suite est géométrique, car il n'y a apparemment pas de raison fixe entre chaque terme

.
Il te faut donc prouver que

, k un réel !
Julie
PS : M'enfin, pas de raison fixe, c'était un peu mal dit : il n'existe pas de réel r tel que
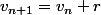
^^
-
emiliey
- Membre Relatif
- Messages: 142
- Enregistré le: 07 Mar 2012, 11:32
-
 par emiliey » 07 Mar 2012, 20:46
par emiliey » 07 Mar 2012, 20:46
globule rouge a écrit:Hello =)
Tu sais bien que
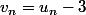
Ainsi,
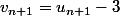
Or il te semble, d'après les résultats du 3)b), que cette suite est géométrique, car il n'y a apparemment pas de raison fixe entre chaque terme

.
Il te faut donc prouver que

, k un réel !
Julie
Bonsoiiiir

Je vais essayer de comprendre ce que vous venez de m'expliquer, merci


-
Peacekeeper
- Membre Irrationnel
- Messages: 1408
- Enregistré le: 19 Jan 2012, 21:34
-
 par Peacekeeper » 07 Mar 2012, 20:47
par Peacekeeper » 07 Mar 2012, 20:47
emiliey a écrit:Bonjour à tous!
Je suis en 1ère ES
Je suis nouvelle sur ce site..
Le problème que j'ai c'est que j'ai un DM de math et il y a un exercice sur les suites que je n'arrive pas à le faire entièrement :/ à partir de la question 3 je bloque.. donc j'aimerai bien avoir un peu d'aide de votre part Svp :$
Voici l'exercice:
on considère la suite Un pour tout n appartenant à N : U0= 2 et Un+1= 2/3Un+1 , pour n appartient à N
1) Calculer u1, u2, u3
2) la suite (Un) est-elle arithmétique ? géométrique?
(a partir de là je n'y arrive plus .. )
3) on définit la suite (Vn) par Vn=Un-3 pour tout n appartient à N
a. calculer V0, V1, V2
b. Déterminer la nature de la suite (Vn)
c. En déduire l'expression de Vn en fonction de n
4) a.Exprimer Un en fonction de Vn, puis en fonction de n
b. Calculer U8
Aidez moi svp :'(
Je vous remercie d'avance, en attendant une réponse assez rapidement de votre part!
Emilie.Y
Rebonsoir,
J'ai lu les échanges avec les précédents intervenants et tu as donc réussi à calculer les V0 V1 et V2 demandés. Tu bloques sur la nature de la suite Vn?

-
Peacekeeper
- Membre Irrationnel
- Messages: 1408
- Enregistré le: 19 Jan 2012, 21:34
-
 par Peacekeeper » 07 Mar 2012, 20:50
par Peacekeeper » 07 Mar 2012, 20:50
globule rouge a écrit:Hello =)
Tu sais bien que
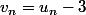
Ainsi,
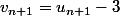
Or il te semble, d'après les résultats du 3)b), que cette suite est géométrique, car il n'y a apparemment pas de raison fixe entre chaque terme

.
Il te faut donc prouver que

, k un réel !
Julie
[HS]
Bah tiens! L'équipe de choc! :p
[/HS]
-
emiliey
- Membre Relatif
- Messages: 142
- Enregistré le: 07 Mar 2012, 11:32
-
 par emiliey » 07 Mar 2012, 20:51
par emiliey » 07 Mar 2012, 20:51
Peacekeeper a écrit:Rebonsoir,
J'ai lu les échanges avec les précédents intervenants et tu as donc réussi à calculer les V0 V1 et V2 demandés. Tu bloques sur la nature de la suite Vn?
Rebonsoir

Euh... oui j'avais trouvé ça :
V0 = U0-3 = 2-3= -1
V1 = U1 -3 = (7/3)-3 = -(2/3)
V2 = U2 -3= (23/9) -3 = -(4/9)
Et oui, je bloque pour les autres questions... :/
-
emiliey
- Membre Relatif
- Messages: 142
- Enregistré le: 07 Mar 2012, 11:32
-
 par emiliey » 07 Mar 2012, 20:52
par emiliey » 07 Mar 2012, 20:52
Peacekeeper a écrit:[HS]
Bah tiens! L'équipe de choc! :p
[/HS]
C'est faut ce que Julie a dit pour que vous dites " HS"?


-
Peacekeeper
- Membre Irrationnel
- Messages: 1408
- Enregistré le: 19 Jan 2012, 21:34
-
 par Peacekeeper » 07 Mar 2012, 20:57
par Peacekeeper » 07 Mar 2012, 20:57
emiliey a écrit:C'est faut ce que Julie a dit pour que vous dites " HS"?

Non, c'est parce que ce que je disais n'avait rien à voir avec le sujet. :p
Cela dit, une suite n'est pas forcément arithmétique ou géométrique. Ce qu'il te faut trouver c'est la relation entre V(n+1) et V(n), tu sais, la relation de récurrence. :p
Mais je vais peut-être laisser la parole à Julie, vu qu'elle a répondu en premier, je ne veux pas m'immiscer dans la démarche qu'elle souhaite te faire suivre.
-
emiliey
- Membre Relatif
- Messages: 142
- Enregistré le: 07 Mar 2012, 11:32
-
 par emiliey » 07 Mar 2012, 20:59
par emiliey » 07 Mar 2012, 20:59
Peacekeeper a écrit:Non, c'est parce que ce que je disais n'avait rien à voir avec le sujet. :p
Cela dit, une suite n'est pas forcément arithmétique ou géométrique. Ce qu'il te faut trouver c'est la relation entre V(n+1) et V(n), tu sais, la relation de récurrence. :p
Mais je vais peut-être laisser la parole à Julie, vu qu'elle a répondu en premier, je ne veux pas m'immiscer dans la démarche qu'elle souhaite te faire suivre.
Ah d'accord

Euh ... comme vous voulez mais je crois qu'elle ne répond plus aha :p
-
emiliey
- Membre Relatif
- Messages: 142
- Enregistré le: 07 Mar 2012, 11:32
-
 par emiliey » 07 Mar 2012, 21:02
par emiliey » 07 Mar 2012, 21:02
Peacekeeper a écrit:Non, c'est parce que ce que je disais n'avait rien à voir avec le sujet. :p
Cela dit, une suite n'est pas forcément arithmétique ou géométrique. Ce qu'il te faut trouver c'est la relation entre V(n+1) et V(n), tu sais, la relation de récurrence. :p
Mais je vais peut-être laisser la parole à Julie, vu qu'elle a répondu en premier, je ne veux pas m'immiscer dans la démarche qu'elle souhaite te faire suivre.
Mais comment vais-je procéder pour démontrer la relation entre V(n+1) et V(n)?


-
Peacekeeper
- Membre Irrationnel
- Messages: 1408
- Enregistré le: 19 Jan 2012, 21:34
-
 par Peacekeeper » 07 Mar 2012, 21:05
par Peacekeeper » 07 Mar 2012, 21:05
emiliey a écrit:Mais comment vais-je procéder pour démontrer la relation entre V(n+1) et V(n)?

Bon, tant qu'elle n'est pas là je t'aide mais si elle souhaite reprendre la parole je la lui laisserai de bon coeur. Julie, si tu me lis...

Tu as la relation entre V(n+1) et U(n+1) ainsi que la relation entre U(n+1) et U(n). Et enfin, de la relation entre V(n) et U(n).
Ecris donc V(n+1) en fonction de U(n) pour commencer.
-
emiliey
- Membre Relatif
- Messages: 142
- Enregistré le: 07 Mar 2012, 11:32
-
 par emiliey » 07 Mar 2012, 21:06
par emiliey » 07 Mar 2012, 21:06
Peacekeeper a écrit:Bon, tant qu'elle n'est pas là je t'aide mais si elle souhaite reprendre la parole je la lui laisserai de bon coeur. Julie, si tu me lis...

Tu as la relation entre V(n+1) et U(n+1) ainsi que la relation entre U(n+1) et U(n). Et enfin, de la relation entre V(n) et U(n).
Ecris donc V(n+1) en fonction de U(n) pour commencer.
D'accord comme voulez

C'est pour répondre à quelle question? :p

-
Peacekeeper
- Membre Irrationnel
- Messages: 1408
- Enregistré le: 19 Jan 2012, 21:34
-
 par Peacekeeper » 07 Mar 2012, 21:08
par Peacekeeper » 07 Mar 2012, 21:08
emiliey a écrit:D'accord comme voulez

C'est pour répondre à quelle question? :p
La nature de la suite (Vn) bien sûr, c'est en trouvant la relation entre V(n+1) et V(n) qu'on saura si elle est arithmétique, géométrique ou rien du tout.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 81 invités
