1ere S puissance d'un point par rapport à un cercle

par **milena75** » 27 Déc 2006, 16:28

bonjour je suis bloquée sur un exercice de mahs depuis 2h. J'espère que vous pouvez m'aider :we:
C est un cercle de centre O et de rayon r et M un point non situé sur C. 2 droites issues de M coupent C respectivement en A et B et en C et D. L'objectif est d'établir que

. On note A' le point diamétralement opposé à A sur le cercle C

1) Démontrer que

2) Démontrer que

=MO²-r²
3) Démontrer que

J'ai réussi la première question :happy2: mais je n'y arrive pas les deux autres :hum:

par **johnjohnjohn** » 27 Déc 2006, 16:54

milena75 a écrit:bonjour je suis bloquée sur un exercice de mahs depuis 2h. J'espère que vous pouvez m'aider :we:
C est un cercle de centre O et de rayon r et M un point non situé sur C. 2 droites issues de M coupent C respectivement en A et B et en C et D. L'objectif est d'établir que . On note A' le point diamétralement opposé à A sur le cercle C

1) Démontrer que
2) Démontrer que =MO²-r²
3) Démontrer que

J'ai réussi la première question :happy2: mais je n'y arrive pas les deux autres :hum:

La question 2 :

Introduis le point O dans le produit scalaire

( Utilise Chasles ). Développe, dis nous si tu vois quelque chose et reviens en causer ici.

par **milena75** » 27 Déc 2006, 17:05

MA.MB=(MO+OA).(MO+OA')
=MO²+ MO.OA' + OA.MO + OA.OA'
j'ai trouvé le MO² mais pas le -r²

par **johnjohnjohn** » 27 Déc 2006, 17:22

milena75 a écrit:MA.MB=(MO+OA).(MO+OA')
=MO²+ MO.OA' + OA.MO + OA.OA'
j'ai trouvé le MO² mais pas le -r²

C'est presque sous tes yeux

Qu'est ce que le point O par rapport au segment AA' ? Quand tu auras répondu à la question, tu sauras facilement en déduire les valeurs respectives des deux expressions :

par **milena75** » 27 Déc 2006, 17:34

O est le milieu de [AA']

et

sont colinéaires de sens contraires et OA=OA' donc le produit scalaire est nul
mais pour

je ne vois pas :hein:

par **tony21** » 27 Déc 2006, 17:39

le produit scalaire est nul si les 2 vecteurs sont perpendiculaires pas lorsqu'ils sont colinéaires. Reprend la définition du produit scalaire
vectOA.vectOA' = Norme de OA*norme de 0A'*cos(vectOA,vectOA')
Norme de OA = Norme de OA' = r
angle (vectOA,vectOA') = pi je te laisse terminer

par **johnjohnjohn** » 27 Déc 2006, 17:47

milena75 a écrit:O est le milieu de [AA']
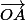
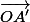
et sont colinéaires de sens contraires et OA=OA' donc le produit scalaire est nul

Certainement pas !!

Pars de cette définition du produit scalaire: Soit a,b deux vecteurs du plan ou de l'espace

a.b=|a|.|b|.cos(a,b) (a,b) mesure principale de l'angle formée par les vecteurs a et b. |a| et |b| les normes des vecteurs a et b.

Applique moi ça aux vecteurs OA et OA' et tu te rendras comptes que ce que tu viens de dire est faux. ( accessoirement , tu auras avancé dans ton exercice )

milena75 a écrit:mais pour je ne vois pas :hein:

Tu ne vois pas ?? O c'est quoi par rapport au segment AA' ?? ( hein bordel de merde !! :lol5: )

Sinon je laisse quelqu'un prendre le relais. A partir de maintenant, je ne suis plus en mesure de te répondre. Je ne pourrai le faire que demain matin.

par **milena75** » 27 Déc 2006, 17:51

= OA*OA'*cos 180= -r²
par contre on ne peut pas calculer vecMO.(OA+OA') on n'a pas la norme du vec MO :hein:

par **tony21** » 27 Déc 2006, 17:55

(OA + OA') = o car vect(A'O) = vect(OA) donc ton expression se simplifie et il te reste MO^2 - r^2

par **mehdisenpai23** » 30 Déc 2019, 13:07

comment on peut demontrer la premier queqtion svp???

1ere S puissance d'un point par rapport à un cercle

1ere S puissance d'un point par rapport à un cercle

Re: 1ere S puissance d'un point par rapport à un cercle

Qui est en ligne