1ère S : nombres dérivés et fonctions usuelles [Résolu]
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
dilemmae
- Membre Naturel
- Messages: 42
- Enregistré le: 27 Déc 2011, 16:40
-
 par dilemmae » 28 Déc 2011, 14:44
par dilemmae » 28 Déc 2011, 14:44
Désolée de te mener la vie dure ! ^^ :marteau:
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 28 Déc 2011, 14:48
par maths0 » 28 Déc 2011, 14:48
Ce qui donne pour les coordonnées de A et B ? :ptdr:
-
dilemmae
- Membre Naturel
- Messages: 42
- Enregistré le: 27 Déc 2011, 16:40
-
 par dilemmae » 28 Déc 2011, 14:48
par dilemmae » 28 Déc 2011, 14:48
Encore une question (si tu en as marre dis le moi :mur: ) :
Pour résoudre le système B, on peut remplacer xB dans l'équation (2). Mais pour le A ? On ne peut rien remplacer...
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 28 Déc 2011, 14:55
par maths0 » 28 Déc 2011, 14:55
Oui car pour le A tu as déjà yA.
Alors tu ne remplaces pas xA dans yA mais l'inverse.
Alors il faut se débrouiller pour trouver xA.
Je te donne la fonction
 = x+5)
.
Soit P un point de la courbe.
Et je te demande de trouver l'abscisse de P sachant que sont ordonnée vaut 0.
-
dilemmae
- Membre Naturel
- Messages: 42
- Enregistré le: 27 Déc 2011, 16:40
-
 par dilemmae » 28 Déc 2011, 15:05
par dilemmae » 28 Déc 2011, 15:05
Pourquoi ai-je fait S ? :cry:
Ben je lis sur l'axe des abscisses xD Honnêtement je sais pas. Je suis désolée.
Faire comme ce qu'on vient de faire, un système avec
y = x + 5
y = 0
donc on peut remplacer 0 = x + 5, x = -5 ?
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 28 Déc 2011, 15:18
par maths0 » 28 Déc 2011, 15:18
Car c'est la même logique !

Si tu as le bleu tu peux avoir le rouge facilement !
Et si tu as le rouge tu peux avoir le bleu avec un peu d'exercice !
Je ne vois pas ce qui te bloque
-
dilemmae
- Membre Naturel
- Messages: 42
- Enregistré le: 27 Déc 2011, 16:40
-
 par dilemmae » 28 Déc 2011, 15:23
par dilemmae » 28 Déc 2011, 15:23
Oui, mais je comprends pas comment tu as réussi a obtenir xp = a².yp + 2a.
Vraiment si tu en as marre dis le, je suis un cas désespéré!
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 28 Déc 2011, 15:33
par maths0 » 28 Déc 2011, 15:33
Avec les opérations élémentaires: Comment tu as fait pour trouver x = -5 avec mon exemple ...
De la même manière !
\\ x = - y{a^2} + 2a \end{array})
-
dilemmae
- Membre Naturel
- Messages: 42
- Enregistré le: 27 Déc 2011, 16:40
-
 par dilemmae » 28 Déc 2011, 16:24
par dilemmae » 28 Déc 2011, 16:24
Bon, alors.

On sait que xB vaut 0, donc si on substitue xb=0 dans yB, on a 2a/a²
C'est pas comme ça qu'il faut faire ?... Parce que je m'embrouille le cerveau la et j'arrive plus à rien. :hein:
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 28 Déc 2011, 16:30
par maths0 » 28 Déc 2011, 16:30
-
dilemmae
- Membre Naturel
- Messages: 42
- Enregistré le: 27 Déc 2011, 16:40
-
 par dilemmae » 28 Déc 2011, 16:37
par dilemmae » 28 Déc 2011, 16:37
Ah ben d'accord c'est simple :doh:
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 28 Déc 2011, 16:38
par maths0 » 28 Déc 2011, 16:38
Pour B oui mais pour A ça l'est un peu moins:
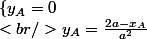
.
-
dilemmae
- Membre Naturel
- Messages: 42
- Enregistré le: 27 Déc 2011, 16:40
-
 par dilemmae » 28 Déc 2011, 16:50
par dilemmae » 28 Déc 2011, 16:50
Ben la on cherche xA. Donc on peut faire :
2a-xa/a² = 0
On fait *a² de chaque côté :
2a-xa = a²
-xa = a² -2a
xa = -a²+2a
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 28 Déc 2011, 16:51
par maths0 » 28 Déc 2011, 16:51
2a-xa/a² = 0
On fait *a² de chaque côté :
2a-xa = a²*0
-
dilemmae
- Membre Naturel
- Messages: 42
- Enregistré le: 27 Déc 2011, 16:40
-
 par dilemmae » 28 Déc 2011, 16:56
par dilemmae » 28 Déc 2011, 16:56
Oups!
2a-xa = a²*0
2a-xa = 0
-xa = -2a
xa = 2a
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 28 Déc 2011, 16:57
par maths0 » 28 Déc 2011, 16:57
A(2a;0) et B(0;2/a) oui !
-
dilemmae
- Membre Naturel
- Messages: 42
- Enregistré le: 27 Déc 2011, 16:40
-
 par dilemmae » 28 Déc 2011, 17:13
par dilemmae » 28 Déc 2011, 17:13
Woaw merci beaucoup !! Au moins j'ai compris ! :id:
Peut on faire la 4 encore ou non? ^^
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 28 Déc 2011, 17:13
par maths0 » 28 Déc 2011, 17:13
Quelles sont les coordonnées de M ?
-
dilemmae
- Membre Naturel
- Messages: 42
- Enregistré le: 27 Déc 2011, 16:40
-
 par dilemmae » 30 Déc 2011, 11:13
par dilemmae » 30 Déc 2011, 11:13
Désolée du retard.
M(a;y)
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 30 Déc 2011, 11:16
par maths0 » 30 Déc 2011, 11:16
? M(a;y(a)) ? donc M(a;...) ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 79 invités

