1ere S D.M limite suite
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
trululu
- Membre Naturel
- Messages: 29
- Enregistré le: 29 Fév 2008, 15:59
-
 par trululu » 29 Fév 2008, 19:34
par trululu » 29 Fév 2008, 19:34
bonjour à tous!
je me suis penché sur un exercice olympiques de maths sur les limites de suites et je suis resté scotché!^^
voici l'énoncé:
Déterminer la limite de la suite (Un) définie par Un= (1-1/2^2) (1-1/3^2) (1-1/4^2) .... (1-1/n^2)
voila j'ai reflechi la dessus mais je bloque vraiment!
si quelqu'un saurait trouver quelquechose ce serait super!
merci d'avance
-
gol_di_grosso
- Membre Irrationnel
- Messages: 1402
- Enregistré le: 22 Sep 2007, 11:28
-
 par gol_di_grosso » 01 Mar 2008, 01:22
par gol_di_grosso » 01 Mar 2008, 01:22
trululu a écrit:si quelqu'un saurait trouver quelquechose ce serait super!
merci d'avance
je trouve
CENSURE
-
trululu
- Membre Naturel
- Messages: 29
- Enregistré le: 29 Fév 2008, 15:59
-
 par trululu » 01 Mar 2008, 10:10
par trululu » 01 Mar 2008, 10:10
ok merci beaucoup mais je ne comprend pas bien comment tu arrives à ce résultat^^
si tu as un peu de temps pourrais tu essayer de détailler un petit peu stp
merci beaucoup
-
gol_di_grosso
- Membre Irrationnel
- Messages: 1402
- Enregistré le: 22 Sep 2007, 11:28
-
 par gol_di_grosso » 01 Mar 2008, 10:28
par gol_di_grosso » 01 Mar 2008, 10:28
tu peux l'écrire comme ça :
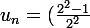\times(\frac{3^2-1}{3^2})\times...\times(\frac{n^2-1}{n^2})\\<br />=(\frac{(2+1)(2-1)}{2^2})\times(\frac{(3-1)(3+1)}{3^2})\times...\times(\frac{(n+1)(n-1)}{n^2})\\<br />=(\frac{(3\times 1)}{2^2})\times(\frac{(4\times 2)}{3^2})\times...\times(\frac{(n+1)(n-1)}{n^2})\\)
tu l'écris avec des factorielles (tu connais ?) au pire tu peux faire sans en simplifiant ta fraction...
après tu simplifie et tu trouve se qu'il faut, enfin normalement
oui ?
-
trululu
- Membre Naturel
- Messages: 29
- Enregistré le: 29 Fév 2008, 15:59
-
 par trululu » 01 Mar 2008, 10:45
par trululu » 01 Mar 2008, 10:45
oui je comprend bien la démarche que tu fais mais je n'ai pas encore vu les factoriels....
Mais si j'ai bien compris il faut que je simplifie la dernière ligne du calcul?
Mais je vois pas en quoi la simplification de cette ligne me permet de trouver le résultat^^!
-
gol_di_grosso
- Membre Irrationnel
- Messages: 1402
- Enregistré le: 22 Sep 2007, 11:28
-
 par gol_di_grosso » 01 Mar 2008, 10:51
par gol_di_grosso » 01 Mar 2008, 10:51
trululu a écrit:oui je comprend bien la démarche que tu fais mais je n'ai pas encore vu les factoriels....
Mais si j'ai bien compris il faut que je simplifie la dernière ligne du calcul?
Mais je vois pas en quoi la simplification de cette ligne me permet de trouver le résultat^^!
ba si :
(3*1)*(4*2)(5*3)*...*((n+1)(n-1)) / ( 2*2*3*3*4*4*...*n*n )
en réordonnant (pour peut-être y voir plus clair)
=(3*4*5*...*(n+1) * (1*2*3*...*(n-1)) / ( 2*3*4*...*n * 2*3*4*...*(n-1)*n )
là il y a quand même beaucoup de simplification à faire, et tu obtient quelque chose de très simple
toujours pas ?
-
trululu
- Membre Naturel
- Messages: 29
- Enregistré le: 29 Fév 2008, 15:59
-
 par trululu » 01 Mar 2008, 11:03
par trululu » 01 Mar 2008, 11:03
si je comprend bien ce que tu fais mais c'est la simplification avec les ... qui me bloque^^
en fait j'y vois pas vraiment clair dans tout ce calcul...
-
gol_di_grosso
- Membre Irrationnel
- Messages: 1402
- Enregistré le: 22 Sep 2007, 11:28
-
 par gol_di_grosso » 01 Mar 2008, 11:09
par gol_di_grosso » 01 Mar 2008, 11:09
trululu a écrit:si je comprend bien ce que tu fais mais c'est la simplification avec les ... qui me bloque^^
en fait j'y vois pas vraiment clair dans tout ce calcul...
par exemple tu as ça à simplifier :
}{(1\times 2 \times 3\times ...\times n)})
tu simplifie, il reste :

je pense que tu dois savoir faire en 1S
sinon comment tu simplifie (2*6*8)/(6*8*7) ? c'est pareil non ?
-
trululu
- Membre Naturel
- Messages: 29
- Enregistré le: 29 Fév 2008, 15:59
-
 par trululu » 01 Mar 2008, 11:12
par trululu » 01 Mar 2008, 11:12
ha ok!!!!
merci beaucoup j'ai saisi le truc ( pas si dur que cela dsl de t'avoir demandé toutes ces question^^')
encore merci :++: :happy2:
-
trululu
- Membre Naturel
- Messages: 29
- Enregistré le: 29 Fév 2008, 15:59
-
 par trululu » 01 Mar 2008, 11:23
par trululu » 01 Mar 2008, 11:23
la limite de Un quand n tend vers + l'infinie est donc:
(+ l'infinie+1)/2
ca tend donc vers + l'infinie
-
gol_di_grosso
- Membre Irrationnel
- Messages: 1402
- Enregistré le: 22 Sep 2007, 11:28
-
 par gol_di_grosso » 01 Mar 2008, 11:26
par gol_di_grosso » 01 Mar 2008, 11:26
trululu a écrit:la limite de Un quand n tend vers + l'infinie est donc:
(+ l'infinie+1)/2
ca tend donc vers + l'infinie
presque, il te manque un n en bas
-
trululu
- Membre Naturel
- Messages: 29
- Enregistré le: 29 Fév 2008, 15:59
-
 par trululu » 01 Mar 2008, 11:32
par trululu » 01 Mar 2008, 11:32
tu veux dire que la reponse c'est pas (n+1)/2 mais (n+1)/2n????
-
gol_di_grosso
- Membre Irrationnel
- Messages: 1402
- Enregistré le: 22 Sep 2007, 11:28
-
 par gol_di_grosso » 01 Mar 2008, 11:46
par gol_di_grosso » 01 Mar 2008, 11:46
oui, tu as n² en bas et tu peux supprimer que n
-
trululu
- Membre Naturel
- Messages: 29
- Enregistré le: 29 Fév 2008, 15:59
-
 par trululu » 01 Mar 2008, 11:51
par trululu » 01 Mar 2008, 11:51
ok moi je trouve comme résultat (n+1)/(2n^2)
-
gol_di_grosso
- Membre Irrationnel
- Messages: 1402
- Enregistré le: 22 Sep 2007, 11:28
-
 par gol_di_grosso » 01 Mar 2008, 11:54
par gol_di_grosso » 01 Mar 2008, 11:54
trululu a écrit:ok moi je trouve comme résultat (n+1)/(2n^2)
en repartant de là :
=(3*4*5*...*(n+1) * (1*2*3*...*(n-1)) / ( 2*3*4*...*n * 2*3*4*...*(n-1)*n )
}{2*3*4*...*n} \times \frac{2*3*...*(n-1)}{2*3*4*...*(n-1)*n}\\<br />=\frac{n+1}{2} \times \frac{1}{n}\\<br />=\frac{n+1}{2n})
-
trululu
- Membre Naturel
- Messages: 29
- Enregistré le: 29 Fév 2008, 15:59
-
 par trululu » 01 Mar 2008, 12:02
par trululu » 01 Mar 2008, 12:02
oui merci c'est ce que je trouve au final^^ (apres plusieurs tentatives^^')
donc la limite quand n tend vers +l'infinie est : 1
-
gol_di_grosso
- Membre Irrationnel
- Messages: 1402
- Enregistré le: 22 Sep 2007, 11:28
-
 par gol_di_grosso » 01 Mar 2008, 12:10
par gol_di_grosso » 01 Mar 2008, 12:10
trululu a écrit:donc la limite quand n tend vers +l'infinie est : 1
non mais tu va vite voir le problème

lim (n+1)/(2n)=
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
