1ére S, coup de pouce sur Barycentre

[SoNnY]

Bonjour, voici l'exo en question :



pour la
1)a) j'ai trouvé AG = 1/3 AB
b) 2MA + MB = 3MG
le reste je suis bloqué, j'espére que vous pourriez m'aider merci !

[Fred_Sabonnères]

Pour que et soient collinéaires,il faut qu'il existe non nul tel que

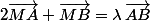
or

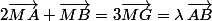
or
donc privé de G



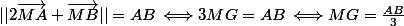
Tu en déduis que Mest sur un cercle de centre ... de rayon...




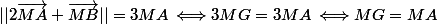
Ca ressemble à la médiatrice ....

[SoNnY]

merci mais comment tu fais pour déterminer le rayon et le contre du cercle ?

[Fred_Sabonnères]

merci mais comment tu fais pour déterminer le rayon et le contre du cercle ?

A et B sont fixes donc
G est fixe
Les points M sont tels que
donc...

[Flodelarab]

merci mais comment tu fais pour déterminer le rayon et le contre du cercle ?

Cherche toujours ce qui est fixe et immuable. Ce sont les léléments concrets auxquels te raccrocher.

Si MG=AB,
AB est connu et fixe,
G est connu et fixe.
M est variable.
Mais on sait que la distance qui le sépare de G est fixe! puisque c'est AB.
L'ensemble des points équidistants d'un même point O est l'ensemble des points du cercle dont le point O (que nous connaissons et qui est fixe, ici) est le centre, et dont le rayon est cette distance.

Quand MA=MG,
A est fixe et connu
G est fixe et connu.
M est variable.
Oui mais il est équidistant de A et de G.
Donc l'ensemble des points équidistants des extrémités d'un segment est ........ (définition de collège)


ok?

[SoNnY]

oui ok merci mais pouvons nous partir de la question 2)a a laquel je suis bloqué ?

[Flodelarab]

Tu ne tombes pas à cheval car ton centre de gravité est porté par le cheval.
Debout, si tu mets sur un pieds, tu dois mettre ton centre de gravité à la verticale de ta jambe pour ne pas te casser la figure.
Ainsi de suite ....

Pour tenir un objet, on est pas obligé de tenir tous les points de cet objet (si l'objet est un solide indéformable) mais seulement sont centre de gravité suffit.
En mathématiques, c'est pareil, sauf qu'on appelle cela un barycentre.
Découpe un triangle dans du papier, trace les médianes, et tu verras que ton triangle tient sur la pointe d'un compas (si tu poses l'intersection des médianes sur la pointe bien sur)


Pour les exo, on va chercher à remplacer les points (affectés d'un certain poids) par le barycentre. Au lieu de dire "nananana avec A et B", on va dire l'équivalent avec le barycentre.
Fred_Sabonnères t'as alors donné une très bonne suite

[SoNnY]

trés bien pour la 2)b dans ce cas il y a bien une méthode de calcul pour trouver l'ensemble des poinst E2 ?

[Flodelarab]

............ c'est exactement pareil. On remplace un ensemble de points embetants par un seul point.

Qu'est ce que tu ne comprends pas dans la soluce de Fred_Sabonnères ?