DM 1ère S : Barycentre et vecteurs .

[Ballon]

Bonjour, je bloque sur un exercice sur le barycentre. Voici l'énoncé :
d est une droite passant par A, distincte de (AB). (vecteur)u est un vecteur directeur de cette droite et M un point tel que (vecteur)AM = (vecteur)u.
d' est la droite parrallèle à d passant par B. Le point N est tel que (vecteur)BN = -2(vecteur)u.
G est le barycentre des points pondérés (A;2) et (B;1).
Démontrer que G est le point d'intersection de (AB) et (MN).

Si vous pouviez me donner quelques pistes pour commencer ... Merci !

[Dinozzo13]

Je réécris tout ça pour y voir plus clair :
, ;
a pour vecteur directeur ;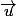
tel que ;
tel que ;
tel que ;
G=bar{(A,2),(B,1)}.

Démontre que et que , prouve ensuite que et ne sont pas parallèles.
En conséquence, les deux droites ne sont pas parallèles mais on un point en commun, le point , point d'intersection de ces deux droites.

[Ballon]

Démontrer que G appartient à [AB], ça c'est fait :)
Mais par contre, comment démontrer que G appartient à [MN] ? Et il ne faudrait pas plutôt démontrer que (vecteur)MG et (vecteur)MN sont colinéaires, de sorte que les points sont alignés ? :id:

[Ballon]

up! :triste: