H^2+0.3h-0.171=0

par **Sophie771** » 26 Juin 2016, 09:54

bonjour a tous,
je ne comprends pas cette equation.
il me semble que c'est une équation du second degré.
le résultat est h=0.290
mais je n'arrive pas trouver ce resultat....
Pouvez vous m'aider je galere depuis des heures....
merci

par **LaDonz** » 26 Juin 2016, 10:02

Salut,
En quelle classe es-tu ? Est ce que tu as vu la méthode du discrimant en cours ?

par **zygomatique** » 26 Juin 2016, 10:19

salut

on multiplie par 100

....

par **Sophie771** » 27 Juin 2016, 16:20

Bonjour merci pour votre réponse...
mais je ne comprends pas la suite ecrite...
comment je retrouve h=0.290???
Pouvez vous détailler votre calcul?
merci

par **Sophie771** » 27 Juin 2016, 16:21

pour le discriminant oui je l'ai vu...mais quand j'applique la formule, je trouve un dicriminant negatif donc sans solution.....c'est ce qui me bloque....
A moins que ce ne soit pas une équation du second degré?
cordialement

par **anthony_unac** » 27 Juin 2016, 16:34

zygomatique a écrit:

....

Vraiment très classe à l'ancienne en exploitant l'identité remarquable de base

. Cette dernière étant normalement connue depuis longtemps par les élèves. :ghee:

Pour ma part je me serai contenter d'essayer de trouver une racine évidente en essayant quelques entiers type avant de conclure :

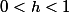
et pis c'est tout !

par **annick** » 27 Juin 2016, 17:26

@zygomatique :

excuse-moi, zygomatique, mais il me semble qu'il y a une petite erreur lorsque tu multiplies par 100 :

h²+0.3h-0.171=0

100h²+30h-17.1=0

Sinon, pour répondre à la question :

100h²+30h-17.1=0

delta= (30)²-4x100x(-17.1)=900+6840=7740

h=(-30+V7740)/200 ou h=(-30-V7740)/200

h=0.290 ou h=-0.590

par **zygomatique** » 27 Juin 2016, 20:08

damned ... je sais plus compter ... :oops:

je corrige ::

zygomatique a écrit:salut

on multiplie par 100

....

et 1935 = 2000 - 65 = 5(400 - 13) = 5 * 387 = 15 * 129 n'est pas un carré parfait ...

par **Sophie771** » 28 Juin 2016, 08:11

Merci a tous pour vos réponses précises...oui je comprends mieux,
mais pourquoi multiplier par 100?
D'habitude pour des équations du second degré je recherche directement le discriminant...
multiplier par 100 permet de faciliter l'équation?

merci

par **zygomatique** » 28 Juin 2016, 08:27

je multiplie par 100 pour trois raisons :

a/ faire disparaître un maximum de nombres décimaux
b/ 100 est un carré parfait
c/ j'obtiendrai le début d'une identité remarquable qui me permettra de factoriser comme au je l'ai appris au collège ... (je n'utilise quasiment jamais le discriminant ... sauf quand je l'enseigne à mes élèves)

en particulier je ne multiplie pas par 1000 qui ferait disparaître tous les nombres décimaux ... mais ferait apparaître une racine carrée ...

H^2+0.3h-0.171=0

h^2+0.3h-0.171=0

Re: h^2+0.3h-0.171=0

Re: h^2+0.3h-0.171=0

Re: h^2+0.3h-0.171=0

Re: h^2+0.3h-0.171=0

Re: h^2+0.3h-0.171=0

Re: h^2+0.3h-0.171=0

Re: h^2+0.3h-0.171=0

Re: h^2+0.3h-0.171=0

Re: h^2+0.3h-0.171=0

Qui est en ligne