Bonjour à la communauté.
J'ai à résoudre un problème de câble suspendu entre deux points (je cherche l'altitude du point bas du câble en fonction de sa longueur et de la position des attaches).
Je suis bien au point en ce qui concerne la partie théorique de l'histoire (développement de l'équation de la courbe de chaînette), mais je me trouve à un moment donné confronté à un système d'équation que l'on ne peut pas résoudre par calcul formel, et qui nécessite une résolution numérique.
N'ayant jamais eu à faire cela, je me tourne alors vers Scilab qui a l'air plutôt puissant et gratuit. Cependant, la puissance de la bête fait que la documentation est pléthorique, et pour résoudre mon problème urgent, je n'ai pas le temps de dépatouiller tout cela et suis donc obligé de solliciter de l'aide...
Voici le système que je dois résoudre :
Je connais D, L et Z, je cherche H. Les équations dont je dispose sont :
1) y = 4*H / (B*L)^2 * x * (B*L - x) (issue de la fonction décrivant la géométrie du câble)
2) B = 2*H / D * (1 - sqrt(1- D / H)) (c'est une constante définie par les conditions initiales)
3) l'intégrale de 0 à L de sqrt(1 + (dy/dx)^2) doit être égale à Z
Merci, si quelqu'un en est capable, de me donner la marche à suivre pas à pas dans scilab pour trouver H en donnant des valeurs à D, L et Z, ou bien de me dire s'il existe un outil plus adapté si ce n'est pas possible.
Je promets qu'en retour, dès que j'aurais eu le temps d'être un peu plus au point, j'apporterais moi aussi ma contribution ici !
Resolution numérique scilab
5 messages
- Page 1 sur 1
bonjour,
en attendant des réponses
voici des liens sur les équations connues sur la chainette
http://www.mathcurve.com/courbes2d/chainette/chainette.shtml
http://www.40tude.fr/blog/chainette/
http://fr.wikipedia.org/wiki/Cha%C3%AEnette
en attendant des réponses
voici des liens sur les équations connues sur la chainette
http://www.mathcurve.com/courbes2d/chainette/chainette.shtml
http://www.40tude.fr/blog/chainette/
http://fr.wikipedia.org/wiki/Cha%C3%AEnette
Merci pour ces liens, que j'avais déjà visité. Mais ces pages ne traitent le sujet que du point de vue purement théorique. Je cherche à établir une approche pragmatique, qui me permette, en ne connaissant que les coordonnées des attaches (pas obligatoirement à la même hauteur), la longueur et la masse linéique du câble, d'en calculer la position du point bas (s'il y en a un) par rapport aux attaches.
C'est dans cet optique que j'aboutit à ce système d'équations, qui a le mérite d'éliminer toutes les grandeurs indéterminées, mais apporte le désavantage de ne pas être soluble de manière formelle.
C'est pourquoi j'ai besoin d'apprendre à le faire dans un solveur numérique.
Cordialement.
C'est dans cet optique que j'aboutit à ce système d'équations, qui a le mérite d'éliminer toutes les grandeurs indéterminées, mais apporte le désavantage de ne pas être soluble de manière formelle.
C'est pourquoi j'ai besoin d'apprendre à le faire dans un solveur numérique.
Cordialement.
Salut,
J'ai pas bien compris d'où sortent tes équations (en particulier la 1em), mais a mon avis, vu ta 3em équation, tu ne t'y pas pris par le bout que j'aurais utilisé.
Si la longueur de ton câble est connue, je pense que tu as grandement intérêt à utiliser la paramétrisation par longueur d'arc de la chainette, c'est à dire = \frac{1}{a} \text{ArgSh}(at+b) + c \\ y(t) = \frac{1}{a}\sqrt{1+(at+b)^2} + d\ \ \ \ \\}) où
où  avec
avec 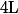 la longueur connue du câble et
la longueur connue du câble et 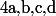 des constantes à déterminer en fonction des extrémités du câble.
des constantes à déterminer en fonction des extrémités du câble.
J'ai pas bien compris d'où sortent tes équations (en particulier la 1em), mais a mon avis, vu ta 3em équation, tu ne t'y pas pris par le bout que j'aurais utilisé.
Si la longueur de ton câble est connue, je pense que tu as grandement intérêt à utiliser la paramétrisation par longueur d'arc de la chainette, c'est à dire
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Salut,
J'ai pas bien compris d'où sortent tes équations (en particulier la 1em), mais a mon avis, vu ta 3em équation, tu ne t'y pas pris par le bout que j'aurais utilisé.
Si la longueur de ton câble est connue, je pense que tu as grandement intérêt à utiliser la paramétrisation par longueur d'arc de la chainette, c'est à dire = \frac{1}{a} \text{ArgSh}(at+b) + c \\ y(t) = \frac{1}{a}\sqrt{1+(at+b)^2} + d\ \ \\}) où
où  avec
avec 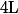 la longueur connue du câble et
la longueur connue du câble et 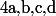 des constantes à déterminer en fonction des extrémités du câble.
des constantes à déterminer en fonction des extrémités du câble.
J'ai pas bien compris d'où sortent tes équations (en particulier la 1em), mais a mon avis, vu ta 3em équation, tu ne t'y pas pris par le bout que j'aurais utilisé.
Si la longueur de ton câble est connue, je pense que tu as grandement intérêt à utiliser la paramétrisation par longueur d'arc de la chainette, c'est à dire
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
