Re: Polynôme

[josias]

Voici un exo facile mais qui me dépasse mais je ne sait pas pourquoi ?
Au marché , trois clientes achètent les même variétés de fruit /
La première achète 2 ananas ,5 mangues et 4 papaye elle paye 620€
La deuxième achète 3 ananas, 5 mangues et 1 papaye elle paye 530€
La troisième achète 2ananas , 7 mangues et 8 papaye
Combinent doit elle payer ?
J'ai poser soit x les ananas, y les mangues et z le papayes
J'obtiens le système suivant :
1) 2x+5y+4z=620
2) 3x+5y+z=530
3) 2x+7y+8z=?
Que faut il mètre a ce niveau pour résoudre le système d'équation a 3 inconnus
Et j'ai oublier de te dire pour hier l'exercice que tu m'a montré etait vrai mais je n'est pas su comment tu a fait pour trouver -2m^2-4m=0
C'est en classe que mes amies et moi Avons chercher a comprendre ton raisonment et sa nous a prit beaucoup de temps donc essaie d'être précis stp

[FLBP]

Bonsoir,

On peut trouver une solution singulière car la matrice P n'est pas inversible (|P| = 0) :


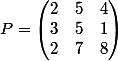
Donc avec la transposée :



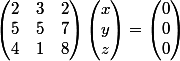
On trouve avec Gauss que :



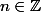
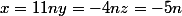
donc :





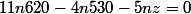
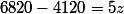
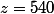
Ton prix est donc de 540.-

Cordialement.

[Ben314]

Salut,
Ben perso., c'est surement pas comme ça que j'aurais fait (ça me semble caricatural du "pourquoi faire simple quand on peut faire compliqué").
Déjà, j'ai un peu du mal à considérer que ça :
(1) 2x+5y+4z=620
(2) 3x+5y+z=530
(3) 2x+7y+8z=?
c'est un système de trois équations à 3 inconnues : de dire que 2x+7y+8z est égal à quelque chose qu'on ne connait pas, je vois franchement pas à quoi ça peut servir; pourquoi ne pas rajouter aussi x+y+z=? (c'est pareil : x+y+z, on sait pas combien ça fait...)

Bref, pour moi, ce qu'on sait, c'est uniquement que
(1) 2x+5y+4z=620
(2) 3x+5y+z=530
Qui est plus ou moins un système de deux équations à 3 inconnues.
Et pourquoi "plus ou moins" ? Ben parce que c'est pas vraiment les valeurs de x,y et z qu'on voudrait connaitre, mais la valeur de =2x+7y+8z (3em facture)

Et à mon avis, là, y'a (au moins) trois méthodes :

I) Soit on résout le plus possible le système et on verra bien ensuite ce qu'on en fait.
Par substitution, (1) donne x=310-5/2y-2z qui injecté dans (2) donne 3(310-5/2y-2z)+5y+z=530 soit encore -5/2y-5z=-400 qui, si on veut continuer par substitution, peut s'écrire y=160-2z.
Le problème, c'est qu'on a pas d'autre équation pour "aller plus loin" et il faut essayer de comprendre le sens de ce qu'on a écrit vu... qu'on peut rien écrire de plus, à part éventuellement que
x=310-5/2y-2z=310-5/2(160-2z)-2z=3z-90 vu qu'on connait y en fonction de z.
Bref, le système se ramène à x=3z-90 et y=160-2z et rien de plus. Et si on réfléchit un peu, ben ça signifie qu'il y a des tonnes de solutions vu qu'on peut prendre n'importe quoi pour z (mais qu'ensuite y'a plus le choix pour x et y).
UNE (et pas LA) solution, ça pourrait par exemple être z=40 ; x=30 ; y=80 ce qui nous donnerais =2x+7y+8z=940.
Mais, une autre solution, ça pourrait être z=50 ; x=60 ; y=60 qui donnerais =2x+7y+8z=940.
Bizarre : ça donne le même résultat...
Est-il possible que, bien qu'on ne puisse pas déterminer les valeurs de x, y et z (y'a des tas de solutions), on puisse quand même déterminer la valeur de =2x+7y+8z ?
Ben c'est pas compliqué à vérifier : on ne connait pas la valeur de z, mais par contre, ce qu'on sait, c'est que x=3z-90 et y=160-2z et ça signifie que =2(3z-90)+7(160-2z)+8z=940 qui, miraculeusement, ne dépend en fait pas de z (les z s'éliminent dans l'équation)

II) Comme en fait, c'est pas les valeurs de x, y et z qui nous intéressent mais celle de =2x+7y+8z, ben c'est clair que ça serait mieux si on avait des équations qui parlent de et pas uniquement de x,y et z.
Sauf que on peut utiliser l'égalité =2x+7y+8z pour écrire par exemple que x=1/2-7/2y-4z de façon à ce que nos deux équations parlent de ,y,z et pas de x,y,z :
(1) 2x+5y+4z=620 => 2(1/2-7/2y-4z)+5y+4z=620 => -2y-4z=620
(2) 3x+5y+z=530 => 3(1/2-7/2y-4z)+5y+z=530 => 3/2-11/2y-11z=530
On procède comme d'hab. par substitution (en gardant pour la fin vu que c'est lui qu'on cherche) : la première donne par exemple y=1/2-2z-310 qui injecté dans la deuxième donne 3/2-11/2(1/2-2z-310)-11z=530 soit encore -5/4=-1175 où il y eu un "miracle" vu que les z ont disparu ce qui fait qu'on peut déterminer la valeur de : =940

III) partant uniquement de
(1) 2x+5y+4z=620
(2) 3x+5y+z=530
Ca parait assez clair qu'on pourra pas trouver la valeur de x, y et z (y'a que deux équations), mais pourtant, il y a quand même des trucs qu'on peut calculer.
Par exemple 4x+10y+8z, on sait que ça va valoir 1240 (on a multiplié la première équation par deux).
On sait aussi que 5x+10y+5z=1150 (on a ajouté les deux équations).
Bref, bien qu'on ne puisse pas calculer x,y et z, y'a quand même certaine expressions ?x+?y+?z qu'on peut calculer (mais pas toutes). Si on réfléchi un peu, on se dit que des trucs qu'on peut calculer, c'est tout ce qui est de la forme a(2x+5y+4z)+b(3x+5y+z) avec a et b réels (qui est évidement égal a620+b530).
Or a(2x+5y+4z)+b(3x+5y+z) = (2a+3b)x+(5a+5b)y+(4a+b)z et vu que ce qu'on aimerait calculer, c'est =2x+7y+8z, on peut se demander s'il existe des réels a et b tels que 2a+3b=2 ; 5a+5b=7; 4a+b=8.
(clairement, il faut "un coup de bol" vu qu'on a trois équations mais que deux inconnues).
Si on résout les deux premières équation 2a+3b=2 et 5a+5b=7 par substitution, on trouve (après calculs) a=11/5 et b=-4/5 et là où il y a "miracle", c'est que la 3em équation 4a+b=8 est effectivement vérifiée.
Et on en déduit bien sûr que =(11/5)620+(-4/5)530=940.

Et si on veut résumé la "philosophie" du bidule, c'est qu'il y a des systèmes qui ne sont pas "suffisant" pour déterminer les valeurs des variables, mais qui permettent quand même de calculer certaine "combinaison" des variable (mais évidement pas toutes : il faut avoir de la chance...
Par exemple ici, si le 3em avait acheté 2ananas , 7 mangues et 7 papaye (au lieu de 8) ben on aurait pas pu savoir combien ça lui a couté.

[Ben314]

Sinon, on peut aussi écrire simplement ça :

La première achète 2 ananas ,5 mangues et 4 papayes elle paye 620€
Donc 22 ananas ,55 mangues et 44 papayes coutent 11x620€ = 6 820€
La deuxième achète 3 ananas, 5 mangues et 1 papaye elle paye 530€
Donc 12 ananas ,20 mangues et 4 papayes coutent 4x530€ = 2 120€

On en déduit que 10 ananas ,35 mangues et 40 papayes coutent 6 820€ - 2 120€ = 4 700€
Et donc que 2 ananas ,7 mangues et 8 papayes coutent 4 700€ / 5 = 940€

Conclusion : La troisième a payé 940 €

Le problème avec cette méthode, c'est évidement de savoir comment on a fait pour trouver le x11 sur la première facture et le x4 sur la deuxième (qui proviennent bien sûr du a=11/5 et b=-4/5 de la 3em méthode présentée dans le post précédent)

[chan79]

salut
on peut essayer de voir ce que ça donne du point de vue géométrique
2x+5y+4z=620
3x+5y+z=530
2x+7y+8z=k
Les deux premières égalités sont des équations de deux plans qui se coupent selon la droite d qui passe par A(150,0,80) et qui est dirigée par le vecteur (-3,2,-1). Ce vecteur est orthogonal au vecteur normal du plan
2x+7y+8z=k qui est donc parallèle à d.
Il est donc nécessaire que ce plan contienne d et donc aussi A:
2*150+7*0+8*80=k donne k=300+640=940

[Black Jack]

Salut,

2x+5y+4z=620 (1)
3x+5y+z=530 (2)
2x+7y+8z=P (3)

(2)-(1)--> x = 3z - 90 (4)
(4) dans (1) --> y = 160 - 2z (5)

(3)-(1) --> 2y + 4z = P-620 (6)

(5) dans (6) --> 320 - 4z + 4z = P-620
P = 940