Calculer coordonnées carre en C
Discutez d'informatique ici !
-
nhella22
- Messages: 5
- Enregistré le: 08 Mai 2010, 15:02
-
 par nhella22 » 08 Mai 2010, 15:09
par nhella22 » 08 Mai 2010, 15:09
Bonjour,
Mon problème est le suivant: j'ai les coordonnées du centre et celle d'un sommet mais je ne sais pas comment retrouvé les trois autres sommets et les codés en C.
Merci d'avance.
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 08 Mai 2010, 15:57
par Arnaud-29-31 » 08 Mai 2010, 15:57
Bonjour,
Une manière simple selon moi est d'exprimer, en utilisant les complexes que si on a O centre du carré, A l'un des sommets, alors B est l'image de A par la rotation d'angle

,
C s'obtient très simplement en exprimant que
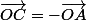
Et D est l'image de C par la rotation d'angle

(ou bien on utilise
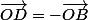
)

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 08 Mai 2010, 16:18
par fatal_error » 08 Mai 2010, 16:18
salut,
une autre méthode aussi :
ton point A(x_A;y_A)
ton point O origine(x_O=0;y_O=0)
tu as un carré ABCD
pour trouver B, tu fais une rot dangle pi/2 (rien de nouveau jusque la).
Tu peux utiliser une matrice de rotation :
 && -sin(\theta) \\<br />sin(\theta) && cos(\theta) <br />\end{pmatrix} \begin{pmatrix}<br />x_A \\<br />y_A<br />\end{pmatrix})
avec tu l'auras deviné, theta qui vaut pi/2
la vie est une fête

-
nhella22
- Messages: 5
- Enregistré le: 08 Mai 2010, 15:02
-
 par nhella22 » 08 Mai 2010, 17:33
par nhella22 » 08 Mai 2010, 17:33
Merci beaucoup
mais comment on calcule OA

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 08 Mai 2010, 17:38
par fatal_error » 08 Mai 2010, 17:38
re,
ben
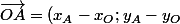)
la vie est une fête

-
nhella22
- Messages: 5
- Enregistré le: 08 Mai 2010, 15:02
-
 par nhella22 » 08 Mai 2010, 17:41
par nhella22 » 08 Mai 2010, 17:41
merci encore d'avoir repondu aussi vite
-
nhella22
- Messages: 5
- Enregistré le: 08 Mai 2010, 15:02
-
 par nhella22 » 19 Mai 2010, 13:30
par nhella22 » 19 Mai 2010, 13:30
bonjour,
Je voulais savoir est-ce que tu saurais comment retrouver les coordonnees des deux autres sommets d'un triangle equilateral a partir du centre du triangle et l'un de ces sommet.
Merci d'avance

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 19 Mai 2010, 13:40
par fatal_error » 19 Mai 2010, 13:40
re,
ben pareil. Tu mets O le centre de ton triangle equilatéral confondu avec l'origine du repère, et tu poses theta = 2pi/3 (ou 120°)
la vie est une fête

-
nhella22
- Messages: 5
- Enregistré le: 08 Mai 2010, 15:02
-
 par nhella22 » 20 Mai 2010, 18:23
par nhella22 » 20 Mai 2010, 18:23
Merci pour ton aide :++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
