Valeur absolue

par **nekros** » 08 Aoû 2006, 21:42

Bonsoir,

Soient

,

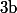
et

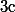
trois réels tels que

,

et

Montrer qu'alors

Bonne réflexion.

Thomas G :zen:

par **aviateurpilot** » 09 Aoû 2006, 02:46

ils existent au moin deux reels parmi a,b et c qui ont le meme signe
on peus alors supposer que a et b ont le meme signe.on a alors

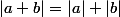
on a

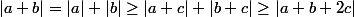
donc

(donc c à un signe different du signe de a et b)
on plus on a

donc

et

donc

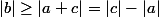
et

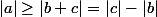
donc

et on a

par suite

|a|+|b|-|c|=0
=>si a et b sont positif alors c est negatif
donc a+b+c=0
=>si a et b sont negatif alors c est positif
donc -a-b-c=0 donc a+b+c=0

par **nekros** » 09 Aoû 2006, 20:21

Bonjour,

Bravo aviateurpilot.

Autre façon :

Supposons que

(rôles symétriques)

Cas 1)

,

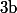
et

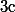
sont de même signe.
Supposons les positifs. (pas de perte de généralité)

On a donc :

,

et

En sommant, il vient que

et par conséquent

Or,

donc

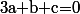Cas 2) L'un des nombres est de signe opposé aux deux autres (bien vu aviateurpilot :++: )

Supposons que

Ainsi, on a :

équivaut à

soit

D'autre part,

implique que

On a donc

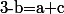
et donc

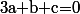
Merci d'avoir participé.

Thomas G :zen:

par **aviateurpilot** » 09 Aoû 2006, 21:18

nekros a écrit:Merci d'avoir participé.

de rien :++:

par **Mohamed** » 10 Aoû 2006, 02:32

slt,voici ma méthode.
en faisant exposer chaque inégalité au carré et en sommant on obtient :

ce qui équivait à

et puisque tout carré est positif on doit avoir a+b+c=0 :zen:

Valeur absolue

valeur absolue

simple

Qui est en ligne