Une somme
Olympiades mathématiques, énigmes et défis
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 25 Aoû 2006, 22:58
par nekros » 25 Aoû 2006, 22:58
Salutations,
Soit
 \in (\mathbb{N^*})^2)
fixé.
On note pour

:
^{i+j}}{i+j}})
Calculer la limite de
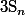
lorsque
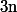
tend ver l'infini.
A+
PS : c'est bien
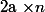
et
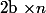
-
El_Gato
- Membre Relatif
- Messages: 313
- Enregistré le: 09 Fév 2006, 17:07
-
 par El_Gato » 25 Aoû 2006, 23:28
par El_Gato » 25 Aoû 2006, 23:28
Déjà pour
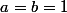
on a, sauf erreur:
^{n+1}}{n+1} + (-1)^n(\frac{1}{n+2} - \frac{1}{n+3} + \cdots + \frac{(-1)^n}{n +n}))
.
Doit y avoir une astuce dans l'exo que j'ai pas vue...
La réponse générale doit probablement dépendre du rapport
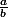
.
PS: Eh Nekros, yoda il aurait pas dit ta citation comme ça. Mais plutôt: "Communs sont commencement et fin, circonférence sur la". Désolée.
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 26 Aoû 2006, 00:04
par nekros » 26 Aoû 2006, 00:04
El_Gato a écrit:PS: Eh Nekros, yoda il aurait pas dit ta citation comme ça. Mais plutôt: "Communs sont commencement et fin, circonférence sur la". Désolée.
C'est vrai, "les paroles de Yoda, telles auraient été" :happy3:
A+
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 26 Aoû 2006, 18:23
par nekros » 26 Aoû 2006, 18:23
Et en remarquant que

?
:happy3:
A+
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 26 Aoû 2006, 18:50
par aviateurpilot » 26 Aoû 2006, 18:50
=\int_0^1\(-\frac{(t^{bn}-1)(t^{an-1}-t)}{(t-1)^2}\))
?
sauf erreur
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 26 Aoû 2006, 18:58
par nekros » 26 Aoû 2006, 18:58
aviateurpilot a écrit:=\int_0^1\(-\frac{(t^{bn}-1)(t^{an-1}-t)}{(t-1)^2}\))
?
sauf erreur
Non, désolé, à moins que la valeur de l'intégrale soit la limite attendue...
Que vaut cette intégrale ?
A+
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 26 Aoû 2006, 19:13
par aviateurpilot » 26 Aoû 2006, 19:13
on a

donc
^{i+j}}{i+j}=\int_0^1(-1)^{i+j}t^{i+j-1}dt=\int_0^1(-1)^{i+j-1}(-1)t^{i+j-1}dt=\int_0^1 -(-t)^{i+j-1}dt)
par suite
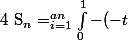^i\(\bigsum_{j=1}^{bn}(-t)^{j-1}\)=\bigsum_{i=1}^{an}\int_0^1-(-t)^i\(\bigsum_{j=0}^{bn-1}(-t)^j\)=\int_0^1\(-\frac{((-t)^{bn}-1)((-t)^{an+1}+t)}{(t+1)^2}\))
sauf erreur
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 28 Aoû 2006, 00:16
par nekros » 28 Aoû 2006, 00:16
Salut,
Pour tout

,
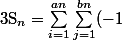^{i+j} \int_0^1 t^{i+j-1} dt=\int_0^1 (\sum_{i=1}^{an} (-1)^it^i)(\sum_{j=1}^{bn} (-1)^jt^{j-1})dt)
Donc
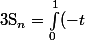 \frac{1-(-1)^{an}t^{an}}{1+t} (-1) \frac{1-(-1)^{bn}t^{bn}}{1+t} dt = \int_0^1 \frac{t}{(1+t)^2} (1-(-1)^{an}t^{an}-(-1)^{bn}t^{bn}+(-1)^{an+bn} t^{an+bn}) dt)
Or,
^2} dt = ln(2)-\frac{1}{2})
D'autre part,
^2} dt|=|\int_0^1 \frac{t}{(1+t)^2}(-(-1)^{an}t^{an}-(-1)^{bn}t^{bn}+(-1)^{an+bn}t^{an+bn}) dt| \le \int_0^1 (t^{an}+t^{bn}+t^{an+bn})dt=\frac{1}{an+1}+\frac{1}{bn+1}+\frac{1}{an+bn+1})
qui tend vers
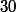
quand
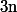
tend vers
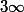
.
On en déduit donc que
-\frac{1}{2}})
A+
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 28 Aoû 2006, 00:27
par aviateurpilot » 28 Aoû 2006, 00:27
tu as trouvé la meme formule de

que moi
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 28 Aoû 2006, 00:53
par nekros » 28 Aoû 2006, 00:53
aviateurpilot a écrit:tu as trouvé la meme formule de

que moi
Salut,
Dans le post 6, je t'avais demandé la valeur de l'intégrale :lol4:
A+
-
El_Gato
- Membre Relatif
- Messages: 313
- Enregistré le: 09 Fév 2006, 17:07
-
 par El_Gato » 28 Aoû 2006, 10:12
par El_Gato » 28 Aoû 2006, 10:12
C'est marrant que ça ne dépende pas de a/b. J'aurais dit le contraire. Très rigolo comme exo.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités