Une répartition des nombres premiers

[Elerinna]

un exercice original suit pour entraîner sa réflexion et le savoir sur les nombres premiers; A votre créativité !

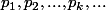
Soit : la suite des nombres premiers consécutifs.

1. Montrer déjà que la suite est infinie.

2. * Préliminaire : montrer que ,
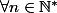
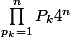
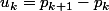
* La suite définie par : est-elle bornée ?

[SaintAmand]

2. * Préliminaire : montrer que ,

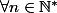
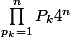
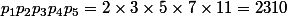
Non. et .

Les autres résultats et cette inégalité (dans sa formulation correcte) sont des classiques.

[Elerinna]

L'énoncé nous donne en fait (la nuance près) : montrer que ,

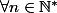
[Le_chat]

C'est pas du tout pareil. Quand tu écris produit pour pk=1 à n, ça veut rien dire vu que (pk) est déjà défin, et par exemple pk;)1.

Et sinon si tu as besoin d'aide sur un dm, tu peux le poster dans la partie supérieur.

[Elerinna]

J'ai retranscrit de tête un problème (modifié) pour être sûre que quelqu'un suivrait. Et s'il est ici, c'est parce que la solution doit pouvoir s'obtenir par plusieurs méthodes : or l'objectif est de viser lesquelles! :lol3:

[emcee]

plus classiquement pour le résultat du 2), il suffit de trouver pour tout M deux nombres premiers consécutifs tels que leur différence est supérieure à M ... et utiliser pour ça l'intervalle [(M+1)!+2 ; (M+1!)+M+1] qui ne contient aucun nb premier.