Une puissance d'une application

[aviateurpilot]

salut les amis


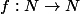
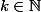
soient une fonction injective et .et

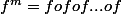
monter que:

si. ou alors

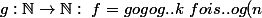N.B: j'ai edité ce post

[ThSQ]

Probablement intéressant mais énoncé pas hyper-clair pour ma petite tête :marteau:

[aviateurpilot]

Probablement intéressant mais énoncé pas hyper-clair pour ma petite tête

si j'explique les données tu va surement trouver le chemin vers la solution :zen:.

la seule chose qui n'est pas hyper clair c'est
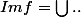
cela signifie que pour
ou

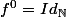
[ffpower]

Je m étais deja amusé a etablir ce resultat de mon coté moi aussi lol.J en avais d ailleurs formulé un corrolaire ainsi:si f est strictement croissante de N dans N,alors l equation f=g^k(au sens des iterees) a des solutions si et seulement si f n est pas au voisinage de l infini une translation par un nombre non multiple de k

En fait on l a deja plus ou moins fait sur un autre topic,sur la resolution de fof(n)=n²(c d ailleurs thsq qui la résolu^^).qd on trouve celle la,on sait normalent faire le cas general...