Une propriété supplémentaire du nombre d'or

[ThSQ]

Très zouli, mais c'est une propriété connue de ces nombres (les nombres de Lucas)

[lapras]

salut
Remarques (premieres impressions sur l'exo)
soit la suite de fibonacci.
On a :

(récurrence pour tout n)
puis on montre que

donc

Puis on doit s'en sortir avec des propriétés arithmétiques

[Timothé Lefebvre]

Salut, j'ai quelque chose en réserve, qui te compare la suite de Lucas et celle de Fibonacci, [url="http://villemin.gerard.free.fr/Wwwgvmm/Iteration/FiboLuca.htm"]ici[/url].

[ThSQ]

Tu as une référence pour les nombres de Lucas ?

Sur l'exxxxcelllent mathworld : http://mathworld.wolfram.com/LucasNumber.html

[lapras]

J'ai donc montré que
avec
Il faut donc montrer que
Ce qui est vrai (je l'ai vu dans le lien de ThsQ) :++: Je ne sais pas si la démonstration est facile.

[Doraki]

On considère la suite d'entiers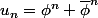
(2,1,3,4,7,11,18,29,...)

Comme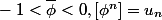 si n est impair.

Si p est un nombre premier différent de 5, dans Z/pZ, cette suite s'écrit toujours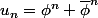 où et 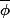sont les solutions distinctes de X²-X-1 dans une extension de Z/pZ.

Alors, toujours dans cette extension, .
Donc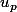 est congru à 1 modulo p.

Si p=5, ben 11 est congru à 1 modulo 5 et ça marche aussi.

[ThSQ]

Tenth line from top :

Rather amazingly, if n is prime, L_n=1 (mod n).

[leon1789]

On considère la suite d'entiers
(2,1,3,4,7,11,18,29,...)

Comme si n est impair.

Si p est un nombre premier différent de 5, dans Z/pZ, cette suite s'écrit toujours où et sont les solutions distinctes de X²-X-1 dans une extension de Z/pZ.

Alors, toujours dans cette extension, .
Donc est congru à 1 modulo p.

Si p=5, ben 11 est congru à 1 modulo 5 et ça marche aussi.

Je pensais aussi à cette preuve.

[Doraki]

On regarde la suite (2,1,3,4,...)
définie par u0 = 2, u1 = 1, et la relation de récurrence u(n+1)=un+u(n-1).

Je suppose p premier>2 (sinon je peux pas diviser par 2 et c'est gênant)

Si p=5, le polynôme X²-X-1 se factorise en (X-3)² dans Z/pZ.
Ici, 1=3*2 donc X-3 est déjà annulateur de la suite,
donc il s'agit en fait de la suite 2*3^n.
up vaut alors 2*3^p = 2*3^1 = u1 = 1 dans Z/pZ.

Si 5 est un carré r² dans Z/pZ, (ex : p=11) le polynôme X²-X-1 se factorise en , où 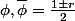dans Z/pZ.
La suite un coincide avec la suite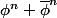 sur les deux premiers termes (c'est fait exprès), et donc ces égalités existent bien dans Z/pZ :


Si 5 n'est pas un carré de Z/pZ, (ex : p=3 ou 7) on se place alors dans le corps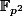 , dans lequel tous les polynômes de degré 2 à coefficient dans Z/pZ sont scindés, et donc qui contient .
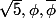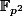est une (Z/pZ)-base de , (pour faire des calculs c'est bien, une base), et dans cette base, .

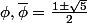Dans ce corps, on a donc encore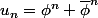 . Le calcul est dans 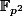mais le résultat est dans Z/pZ.
Et donc on a toujours dans 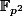, et donc le résultat est vrai dans Z/pZ.

[lapras]

Y aurait il une démonstration élémentaire du fait que ma suite (qui est celle de doraki) ?
D'où peux tu dire que dans Z/pZ ?

[Doraki]

Théorème de Frobenius, les coefficients binomiaux qui sont impliqués dans le développement de sont tous multiples de p.

[lapras]

Oui je sais, mais bon n'est pas entier... Donc on ne peut pas bosser comme d'habitude dans Z/pZ, non ?