Une de mes plus belles ennigmes

[ffpower]

Euh,je suis pas d accord,la strategie ne dépend pas du nombre de cow boys.

[Imod]

J'ai enfin compris :marteau: :marteau: :marteau: :marteau:

Le dernier cowboy envoie un élément descriptif des couleurs des chapeaux qu'il voit et dont la variation au cours du "jeu" dépend de façon univoque de la couleur des chapeaux annoncer par chacun des "joueurs" précédents . Chacun suit alors les évolutions de cet élément qu'il peut comparer à ce qu'il voit ...

Je ne donne pas l'élément descriptif tellement il est simple :zen:

C'est vraiment bête quand on a compris :triste:

Imod

PS : ça marche avec un nombre quelconque de cowboys et de couleurs de chapeaux .

[scelerat]

PS : ça marche avec un nombre quelconque de cowboys et de couleurs de chapeaux .

Flute alors, ma solution ne serait pas la meilleure ?
Je detaille donc ma solution : le cowboy de l'arriere indique, par la couleur qu'il enonce, la parite des nombres de chapeaux de chaque couleur. Sauf que ces parites sont au nombre de 4, ce qui fait 16 combinaisons possibles (ou 4 bits), et qu'il ne peut donner que l'equivalent d'un nombre de 0 a 3, soit 2 bits.
A partir des 4 parites, chaque cowboy peut deviner la couleur de son chapeau puisque c'est celle qui differe de ce qu'il compte devant lui. A partir de deux parites, je ne vois qu'une maniere dont il peut s'en sortir : la moitie des configurations de depart sont eliminees par la connaissance de la parite du total et les cowboys conviennent que celui de l'arriere annoncera la meme couleur pour les configurations complementaires (dans le cas pair 0101 et 1010, 1100 et 0011, 0000 et 1111, 1001 et 0110), et chaque cowboy peut discriminer entre les deux configurations complementaires mises a jour a son niveau puisque la bonne differe d'un bit et l'autre de trois par rapport a ce qu'il voit devant lui.

Edit: Ca peut effectivement marcher avec un nombre quelconque de cowboys, le cowboy peut eliminer aussi les deux configurations complementaires qui n'ont pas la bonne parite totale. Je ne vois pas comment ca peut marcher avec 6 couleurs, par contre.

[Imod]

Edit: Ca peut effectivement marcher avec un nombre quelconque de cowboys, le cowboy peut eliminer aussi les deux configurations complementaires qui n'ont pas la bonne parite totale. Je ne vois pas comment ca peut marcher avec 6 couleurs, par contre.

Il suffit d'attribuer un numéro 0 à n-1 à chacune des n couleurs , de compter chaque chapeau avec le coefficient correspondant à sa couleur puis de prendre le reste modulo n .

Imod

[Doraki]

N'importe quel groupe d'ordre n convient.

Moi au début j'ai pensé à convertir les couleurs en binaire et à faire du XOR
dessus, ça correspond à utiliser le groupe (Z/2Z)².

J'aurais trouvé moins vite si ça avait été 5 ou 3 couleurs.

[Anonyme]

J'ai rien compris a votre solution quelqu'un peut mieux expliquer ?

[Imod]

Beaucoup de complications pour peu de choses .

Supposons qu'il y a m cowboys 1 ; 2 ; ...; m ( 1 est le premier ... ) et n couleurs 0; 1 ; ...; n-1 . Chaque cowboy k fait la somme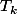 des couleurs des chapeaux devant lui . Le mième trouve 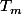et l'annonce ( modulo n ) ensuite il a de grandes chances de perdre la vie mais sauve celle de tous les autres . Le cowboy m-1 calcule et en déduit la couleur de son chapeau qui est modulo n les autres cowboys calculent alors modulo n . Le cowboy m-2 calcule et en déduit la couleur de son chapeau qui est modulo n , les autres cowboys calculent modulo n ...

Imod

[scelerat]

Il suffit d'attribuer un numéro 0 à n-1 à chacune des n couleurs , de compter chaque chapeau avec le coefficient correspondant à sa couleur puis de prendre le reste modulo n .

Imod

Bravo ! Finalement, l'histoire de l'ogre et des nains m'a plutot egare vers un truc complique et pas optimal.

[Imod]

Finalement, l'histoire de l'ogre et des nains m'a plutot egare vers un truc complique et pas optimal.

Je ne devrais pas le dire mais je n'avais pas lu le fil jusqu'au bout :hum: Je sais c'est mal :triste:

Imod

[charlol]

Ta solution ne marche pas scelerat :) c'est surtout ça le problème... (c'est compliqué :s)
Alors, elle est pas belle mon énigme?

[Patastronch]

Ta solution ne marche pas scelerat c'est surtout ça le problème...

Sa solution marche tres bien mais assure que n-2 survivants sur, n-1 survivants avec une chance sur 4 et n survivants avec une chance sur 16.

Soit une espérance de 1/16 *n + 3/16 * (n-1) + 12/16 * (n-2) = n - 27/16 survivants.

La méthode d'Imod (qui améliore l'idée de scélerat au fond) donne une espérance de 1/4*n + 3/4 * (n-1) = n-3/4 survivants.

La méthode de Scélerat marche très bien mais comme il le dit elle n'est pas optimale. Et on est sur que celle d'Imod est optimale puisque le premier ne peut pas modifier sa probabilité de survie qui est de 1/4 et cela quelque soit la stratégie adoptée.

[scelerat]

Ta solution ne marche pas scelerat c'est surtout ça le problème... (c'est compliqué :s)
Alors, elle est pas belle mon énigme?

Avec 4 couleurs, elle n'est pas elegante mais elle marche parfaitement.
Ton enigme est tres belle, et l'aurait ete encore plus avec les 7 couleurs de l'arc-en-ciel (a mon avis) :happy2:

[scelerat]

Sa solution marche tres bien mais assure que n-2 survivants sur, n-1 survivants avec une chance sur 4 et n survivants avec une chance sur 16.

n-1 survivants surs, et n avec une chance sur 4.
Le cow-boy de rang r a acces aux 4 parites : 2 par l'information donnee par le dernier cow-boy et mise a jour, une par la parite de r, et la derniere du fait qu'une seule parite peut changer entre lui et ce qu'il voit devant lui.
Par exemple, la couleur donnee par le dernier cow-boy signifie dans leur convention que ce qu'il voit est une des 4 configurations {PIPP,IPII,PPII,IIPP}. Le 39e cow-boy sait que 39 est impair, donc que le choix n'est qu'entre PIPP et IPII. Devant lui, il ne peut voir que IIPP, PPPP, PIIP, PIPI, PPII, IIII, IPPI ou IPIP puisque 38 est pair. S'il voit mettons IPPI, il sait que la sienne ne peut pas etre PIPP, donc c'est IPII et la couleur de son chapeau est la troisieme (et il en est sur).

[scelerat]

La méthode d'Imod (qui améliore l'idée de scélerat au fond)...

Je ne le vois pas comme ca. Si l'on revient a l'enigme avec les chapeaux blancs ou noirs, c'est la maniere dont on generalise la parite a m couleurs qui differe. J'ai generalise en cherchant les m parites des nombres de chaque couleur, tandis qu'Imod a generalise la parite qui est aussi la somme modulo 2, et donc a m couleurs il prend la somme modulo m. Beaucoup plus elegant, comme je l'ai deja reconnu.

[gnarfk]

Flute alors, ma solution ne serait pas la meilleure ?
Je detaille donc ma solution : le cowboy de l'arriere indique, par la couleur qu'il enonce, la parite des nombres de chapeaux de chaque couleur. Sauf que ces parites sont au nombre de 4, ce qui fait 16 combinaisons possibles (ou 4 bits), et qu'il ne peut donner que l'equivalent d'un nombre de 0 a 3, soit 2 bits.
A partir des 4 parites, chaque cowboy peut deviner la couleur de son chapeau puisque c'est celle qui differe de ce qu'il compte devant lui. A partir de deux parites, je ne vois qu'une maniere dont il peut s'en sortir : la moitie des configurations de depart sont eliminees par la connaissance de la parite du total et les cowboys conviennent que celui de l'arriere annoncera la meme couleur pour les configurations complementaires (dans le cas pair 0101 et 1010, 1100 et 0011, 0000 et 1111, 1001 et 0110), et chaque cowboy peut discriminer entre les deux configurations complementaires mises a jour a son niveau puisque la bonne differe d'un bit et l'autre de trois par rapport a ce qu'il voit devant lui.

Edit: Ca peut effectivement marcher avec un nombre quelconque de cowboys, le cowboy peut eliminer aussi les deux configurations complementaires qui n'ont pas la bonne parite totale. Je ne vois pas comment ca peut marcher avec 6 couleurs, par contre.

il y a un gros problème avec cette solution : le premier cow-boy voit 39 (40- lui) camarades . et donc il y aura tjrs 1 ou 3 couleurs représentées en nombre impair devant lui .
on peut essayer d'adapter ta solution en faisant dire au premier cow boy la seule couleur représentée en nombre pair , ou la seule représentée en nombre impair . ce qui permet aux autres de trouver leur couleur .

Mais cette solution a pour gros défaut par rapport à celle que je connais de ne pas s'adapter facilement à tout nombre de cow boys et tout nombre de couleurs .

[Patastronch]

Je ne le vois pas comme ca. Si l'on revient a l'enigme avec les chapeaux blancs ou noirs, c'est la maniere dont on generalise la parite a m couleurs qui differe. J'ai generalise en cherchant les m parites des nombres de chaque couleur, tandis qu'Imod a generalise la parite qui est aussi la somme modulo 2, et donc a m couleurs il prend la somme modulo m. Beaucoup plus elegant, comme je l'ai deja reconnu.

Bon j'avais mal capté ta solution je crois.
Voila ce que j'avais compris :
Le premier va donner la parité des chapeaux rouge et bleu sur l'ensemble des 38 chapeaux (Les 40 sauf le sien et celui qui est devant lui). Le second va donner la parité des 2 autres couleurs sur l'ensemble des 38 chapeaux. Et après tout va tout seul.
Voila pourquoi j'avais calculé une espérance de survie de n-27/16 et que je disais que la solution d'Imod optimisait cette solution.

[scelerat]

il y a un gros problème avec cette solution : le premier cow-boy voit 39 (40- lui) camarades . et donc il y aura tjrs 1 ou 3 couleurs représentées en nombre impair devant lui .

Ca n'est pas vraiment un probleme, ca permet de diviser par deux le nombre de cas possibles.

Mais cette solution a pour gros défaut par rapport à celle que je connais de ne pas s'adapter facilement à tout nombre de cow boys et tout nombre de couleurs .

Exact pour le nombre de couleurs, mais bon, il y a des situations ou il est essentiel d'avoir une solution, et ou son elegance et son optimalite sont plus secondaires. :zen:

[vanhoa]

voila, j'ai simplement lu les premiers messages et je ne voudrais surtout pas lire trop loin de peur de tomber sur un gros indice.

selon les contraintes du problemes, les cowboys vont se concerter et une fois mis en file indienne, le dernier (celui qui voit tout le monde) parlera en premier et la SEULE chose qu'il pourra dire est soit rouge, bleu, vert ou jaune. sans modulation de voix et il n'a pas le droit de ne rien dire c'est ca?

(est ce qu'il a le droit de donner sa reponse au bout de tant de secondes? je veux dire par la, est ce que le temps avant de donner sa reponse peut entrer en compte?

merci (je sais qu'il y en a qui connaissent la solution)

++

[vanhoa]

car j'avais pense a une forme de raisonnement qui serait le suivant:

si on commence au dernier prisonnier, soit le 40eme, le nieme prisonnier pourrait donner le nom d'une couleur qui donnerait une information au n-1eme et n-2eme comme par exemple, si on prend l'ordre des couleurs rouge-bleu-vert-jaune, en disant "bleu" cela signifierai que les deux suivant ont des chapeaux qui auraient 2 couleurs qui se suivent comme rouge-bleu, bleu-vert, vert-jaune ou jaune-rouge (selon l'ordre des couleurs qu'ils auraient defini)

mais seulement cela ne marche pas car apres le premier a parler, les autres sont oblige de citer leur propre couleur et donc ne peuvent pas donner d'informations aux autres.

c'est pour ca que je pensais que l'information ne doit pas resider dans le nom de la couleur mais plutot dans l'attente (le temps qu'il met a dire sa propre couleur)

donc ma question: est ce que c'est bien de penser que l'information n'est pas dans la couleur enoncee?

[ffpower]

Non, ya pas de gruge de ce genre, toute l'info est donnée pas la couleur énoncée..