Une histoire de Q et d'intervalles

[DamX]

Bonjour à tous,

Un petit fun fact que j'ai vu passer. Je ne sais pas si c'est classique ou non.

Peut-on trouver une réunion dénombrable d'intervalles ouverts de qui contienne tout en étant de mesure finie ?

Damien

[MacManus]

Salut,

la réponse est oui. mais j'ai triché car j'ai trouvé une preuve sur internet. mais la méthode est assez intuitive après coup.

[DamX]

Oui, j'ai aussi une solution qui est intuitive "après coup", quand on l'a déjà vue, je suppose que c'est la même :p

Bref pour les autres, comme la réponse est oui le défi devient plus formellement et simplement :

Trouver une suite d'intervalles ouverts de telle que et

[adrien69]

Une solution à laquelle j'ai pensé comme un grand :

On numérote les éléments de Q via une bijection (classique ou non, on s'en fout) avec N*

Et on prend pour chaque q_n l'intervalle
Et puis c'est fini.

[DamX]

Bravo !

et on peut rendre la mesure aussi petite qu'on veut en ajustant un coeff, rien de choquant vu que Q est de mesure nulle, mais je trouve ça tout de même assez intéressant comme résultat.

[adrien69]

C'est contre-intuitif au vu de la densité de Q, et que si on a envie de prendre un intervalle autour de chaque rationnel, ben on a vite fait de se dire que la réunion est R.

Mais c'est oublier que les contre-exemples de "dense=mesure pleine" existent à foison.

[adrien69]

C'est la même preuve que vous ?

[DamX]

C'est la même preuve que vous ?

oui oui, j'avais qn +/- 1/2^n mais c'est pareil.

C'est pas tant le côté contre-exemple de "dense=mesure pleine" que je trouve intéressant que le fait que ce sont des intervalles, qui sont "continus" et contiennent chacun une infinité de rationnels et d'irrationnels, et arriver à recouvrir Q avec des intervalles sans recouvrir tout R est de prime abord assez contre-intuitif, on laisse en fait beaucoup de trous ponctuels qui font l'essentiel de la masse.

[adrien69]

En fait on voit le même côté bizarre, on ne le formule pas de la même façon, c'est tout ;)

[MacManus]

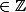
j'ai vu une preuve (un peu plus subtile mais dans le même ordre idée) avec comme intervalle ouvert , avec p et q>0 et une suite de réels strictement positifs.

...

[DamX]

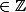
j'ai vu une preuve (un peu plus subtile mais dans le même ordre idée) avec comme intervalle ouvert , avec p et q>0 et une suite de réels strictement positifs.

...

euh il doit manquer une condition sur la suite parce que si on prend u_n=1, ca donne R tout entier...

[adrien69]

Même si elle ne fait que tendre vers 0 c'est mort.

[MacManus]

euh il doit manquer une condition sur la suite parce que si on prend u_n=1, ca donne R tout entier...

glurp ...!

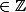
, avec p et q>0 et une suite de réels strictement

positifs telle que , avec eps>0.

- Déterminer la longueur de l'intervalle
- Montrer que la somme des longueurs des intervalles vaut au plus
- En déduire une expression de la suite , pour que la mesure de l'union des intervalles soit finie.

[Ezra]

glurp ...!

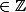
, avec p et q>0 et une suite de réels strictement

positifs telle que , avec eps>0.

- Déterminer la longueur de l'intervalle
...

Si on appelle la longueur de l'intervalle cherché, peut-on le majorer par : , avec : , ?

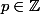
[MacManus]

Salut,
Oui, tu as raison:
Maintenant, il faut majorer l'expression

[ARIMA]

Bonjour,
c'est ce que l'on appelle la séparabilité...

C'est une propriété fondamentale de R^n qui permet d'avoir des résultats très puissants en analyse.

Tu peux généraliser ce résultat dans les espaces séparables avec des hypothèses raisonnables sur la mesure.