Une formule pour les nombres premiers
Olympiades mathématiques, énigmes et défis
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 03 Déc 2010, 13:54
par benekire2 » 03 Déc 2010, 13:54
Euler 07 a écrit:J'espère ne jamais rencontrer une formule pareil de ma vie :dodo:
Ba tient , je t'avais zappé , mais tu peut tout a fait prendre ce défi , en admettant les deux lemmes , OU en en admettant un seul OU en faisant l'exo de Ben et en en admettant aucun ... je te promet que c'est pas un machin "parachutté" ou totalement astucieux ...

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 03 Déc 2010, 17:06
par Ben314 » 03 Déc 2010, 17:06
Bon, je viens de passer une plombe à regarder s'il y avais pas moyen de faire un peu mieux pour la constante Kn de mon dernier post en améliorant les majorations.
Tout ce que j'ai trouvé, c'est ça :
On enlève la question 2) et, à la place, on montre à l'aide du 1) que pour tout
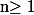
\leq\ln(16)\frac{n}{\ln(n+1)} $)
.
On utilise cette majoration au 4) pour obtenir
}$)
qui est un peu meilleur que la majoration de l'exo.
On obtient alors la minoration demandée pour
-\pi(n)$)
dés que
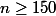
(environ) ce qui est légèrement mieux que 4073, mais il reste 150 vérif à faire "à la main" et c'est un peu con...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 03 Déc 2010, 17:26
par Sylviel » 03 Déc 2010, 17:26
Comment ça 150 vérif ? Tu veux dire vérifier le postulat de Bertrand pour n=<150 ? Cela se fait en vérifiant que quelques nombres bien choisit sont premiers...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 03 Déc 2010, 17:32
par Ben314 » 03 Déc 2010, 17:32
[quote="Sylviel"]Comment ça 150 vérif ? Tu veux dire vérifier le postulat de Bertrand pour n=\frac{n}{3\ln(n)}[/TEX] ce qui est quand même nettement plus fort que Bertrand et il faut le vérifier pour une bonne proportion des n tels que 2n-1 soit premier.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 03 Déc 2010, 17:56
par benekire2 » 03 Déc 2010, 17:56
Sii on veut juste demontrer le postulat de bertrand une chaine de landau devrait suffire. Enfin je suppose que c est pas ca que tu veut...
Edit:hrillé deux fois!
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 03 Déc 2010, 18:07
par Sylviel » 03 Déc 2010, 18:07
Ok j'ai rien dit, je suis juste de loin la discussion...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
zygote3333
- Membre Naturel
- Messages: 13
- Enregistré le: 03 Déc 2010, 18:08
-
 par zygote3333 » 03 Déc 2010, 21:00
par zygote3333 » 03 Déc 2010, 21:00
Moi j'ai beaucoup plus simple pour trouver les nombres premiers. Regardez dans la partie café.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 03 Déc 2010, 21:11
par Ben314 » 03 Déc 2010, 21:11
zygote3333 a écrit:Moi j'ai beaucoup plus simple pour trouver les nombres premiers. Regardez dans la partie café.
Sauf que
1) Le but ici n'est absolument pas de trouver des nombres premiers.
2) "Ta" méthode, elle est archi connue depuis 200 avant J.C.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 05 Déc 2010, 11:49
par benekire2 » 05 Déc 2010, 11:49
Donc personne n'a envie de s'y attaquer au problème initial ?? ( les "grands" exclus )
Si c'est le cas je poste une solution dans l'après midi.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 06 Déc 2010, 19:36
par benekire2 » 06 Déc 2010, 19:36
Bon, je ne détaille pas trop la démo mais ceux qui s'y intéressent n'auront pas trop de mal a s'en sortir, au pire ca fait un petit exo, le plan de la preuve :
- On montre vie le postulat de Bertrand que
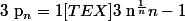
et pour faire 1 il suffit que
} \rfloor >1)
puisque via [2] on sait que le passage à la racine n-ième assure qu'on ne dépassera jamais 1 . Cela se produit donc quand
 \le n-1)
i.e tant que
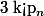
, et au final , la somme ( la grande ) , qui contient forcément le nième nombre premier via [1] , vaut
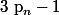
et on conclu .
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 06 Déc 2010, 22:14
par ffpower » 06 Déc 2010, 22:14
Utiliser le postulat de Bertrand pour montrer que p_n<2^n, ça m'a l'air un peu fort de café :we:
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 06 Déc 2010, 22:22
par Doraki » 06 Déc 2010, 22:22
Cette formule elle est dans "merveilleux nombres premiers" de JP Delahaye.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 06 Déc 2010, 22:27
par benekire2 » 06 Déc 2010, 22:27
ffpower a écrit:Utiliser le postulat de Bertrand pour montrer que p_n<2^n, ça m'a l'air un peu fort de café :we:
Ben perso j ai procede par recurrence et dans l heredite j ai besoin de bertrand. As-tu quelque chose de plus simple en tête?
Ca m'intéresse, merci!
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 06 Déc 2010, 22:36
par Doraki » 06 Déc 2010, 22:36
on peut obtenir un majorant du n-ième nombre premier calculable avec la suite
u1 = 2, u(n+1) = u1*u2*...*un + 1 = un*(un-1)+1.
u(n+1) est premier avec u1,u2...un donc il contient un facteur premier distinct de tous ceux qu'on a pris avant.
c'est facile de montrer que un <= 2^(2^(n-1)), et donc que pn <= 2^(2^(n-1))
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 07 Déc 2010, 00:20
par ffpower » 07 Déc 2010, 00:20
benekire2 a écrit:Ben perso j ai procede par recurrence et dans l heredite j ai besoin de bertrand. As-tu quelque chose de plus simple en tête?
Ca m'intéresse, merci!
Disons qu'au vu de la majoration fine obtenue par l'exo de Ben, le pn10 ( je dis au hasard, à vérifier^^ ), ce qui donne
>\sqrt{n/2})
et donc
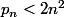
pour n plus grand que 20, ce qui est déjà bien meilleur que

, sans trop me fouler. Et à mon avis on doit pouvoir faire du plus grossier ( bon, un peu moins que Doraki^^ ) pour majorer plus facilement en

..
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 07 Déc 2010, 18:15
par benekire2 » 07 Déc 2010, 18:15
Bon, en fait je suis pas méga convaincu puisque tu réutilise la moitié de la preuve de Bertrand ... :ptdr: et moi je pensais que tu allais me sortir un truc genre astucieux mais trivial ...
Doraki : Le hic c'est que je demande 2^n et pas 2^(2^(n-1)) qui est bien plus grossier ...
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 07 Déc 2010, 21:59
par Doraki » 07 Déc 2010, 21:59
benekire2 a écrit:Doraki : Le hic c'est que je demande 2^n et pas 2^(2^(n-1)) qui est bien plus grossier ...
Certes mais bon, adapter la formule ne demande absolument aucun effort et c'est pas comme si elle était un tantinet utilisable à la base.
Le postulat de bertrand est utilisé juste pour avoir un majorant de pn donc autant s'en passer en prenant un truc grossier mais simple au niveau de la preuve.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 07 Déc 2010, 22:15
par benekire2 » 07 Déc 2010, 22:15
Oui je suis d accord avec toi doraki! mais bon,en l occurence on voulait justifier que le n ieme nombre premier est inferieur a 2^n. ...
-
docneurone
- Messages: 1
- Enregistré le: 26 Déc 2010, 11:41
-
 par docneurone » 26 Déc 2010, 11:48
par docneurone » 26 Déc 2010, 11:48
bonjour a tous, j'ai un exercice, dans le même style que celui proposé:
je dois montrer que C^n_2n (n parmi 2n)> n^(p(2n)-p(n)) , ou p(n) désigne le nombre dentier premiers compris au sens large entre 2 et n. et que C^n_2n< ou égal à (2n)^p(2n)
pour la premiere inégalité j'essaie à partir de (2n)!=C^n_2n*n!*n!
mais je ne vois pas trop comment procéder.
merci d'avance!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
