Une formule pour les nombres premiers
59 messages
- Page 2 sur 3 - 1, 2, 3
par Anonyme » 01 Déc 2010, 17:53
benekire2 a écrit:
Sinon, pour la minoration 3a ba d'habitude je minore par 4^n/(2n+1) et pour l'affiner je bourrine, rien de plus.
Je vois mal en quoi cette minoration est utile puisqu'elle est moins "precise" que celle de l'inegalite. Peux tu me montrer comment tu t'en est sorti ?
par benekire2 » 01 Déc 2010, 18:08
Qmath a écrit:Je vois mal en quoi cette minoration est utile puisqu'elle est moins "precise" que celle de l'inegalite. Peux tu me montrer comment tu t'en est sorti ?
C'est bien ce que j'ai dit , j'utilise une minoration moins précise quand je travaille avec des minorations de coefficients binomiaux.
Pour la version "précise" il te suffit d'étudier les variations de la suite post de 12h52
Sinon, une quetion comment as-tu procéder pour la 1 ?
par Anonyme » 01 Déc 2010, 18:33
Pour la 1/ j'ai procédé comme toi et ben sauf que je pense que c'est le cas impair qui est trivial et non le cas ou n est pair puisque l'inegalite p
J'ai presque jamais travailler avec des coefficients binomiaux donc je sais pas s'il est courent de minorer avec quelque chose de moins precis pour obtenir quelque chose de plus précis.
Je regarde ton post ..
J'ai presque jamais travailler avec des coefficients binomiaux donc je sais pas s'il est courent de minorer avec quelque chose de moins precis pour obtenir quelque chose de plus précis.
Je regarde ton post ..
par Ben314 » 01 Déc 2010, 18:55
Bon, pour la 6), j'ai bien recopié le bon énoncé (je n'ai pas fait cet exo depuis un moment, mais j'ai quelques corrections de fautes de frappes dans les exos autour, donc s'il y avait une erreur, je pense que je l'aurais corrigée...)
La formule que l'on obtient à la fin permet de donner un encadrement de pi(n) avec des truc du style cst.ln(n)/n, mais ne permet pas de conclure que pi(n) est équivalent à ln(n)/n (théorème des nombres premiers)
après, quand je dit "majorer à la va vite", je veut dire qu'à peu prés partout, tu peut prendre des majorants/minorants un peu plus grossiers (et donc plus faciles à obtenir) voire même faire des études asymptotique pour en déduire que "à partir d'un certain rang on a ..." (ce qui souvent est plus simple) et que dans ce cas, tu obtient à la fin des constantes un peu moins bonnes que le 1/3 et le ln(4) ou bien uniquement une inégalité vraie "à partir d'un certain rang".
L'exo. est très calculatoire du fait qu'on veut obtenir à la fin des "vraies" constantes pas trop grandes et un inégalité valable pour tout n et pas seulement "à partir d'un certain rang".
De mémoire, historiquement parlant, il y a eu beaucoup de tentatives pour "raffiner" des formules de ce genre et essayer d'en déduire le théorème des nombres premiers, mais il me semble que toutes sont restées infructueuse...benekire2 a écrit:- Les ln(n)/n me rappelle le théorème des nombres premiers ( dont j'ai pas encore lu la preuve mais ça peut attendre :zen: ) on pourrait pas le "déduire" de ça ou alors c'est vraiment autre chose ? ( Je n'y ai pas trop réfléchi, il se pourrait donc que ma question soit totalement stupide)
- Ben, quand tu dit "majorer à la va vite" de quoi tu veut parler ?? J'ai essayé mais je dois encore montrer queest faux pour n suffisamment grand
La formule que l'on obtient à la fin permet de donner un encadrement de pi(n) avec des truc du style cst.ln(n)/n, mais ne permet pas de conclure que pi(n) est équivalent à ln(n)/n (théorème des nombres premiers)
après, quand je dit "majorer à la va vite", je veut dire qu'à peu prés partout, tu peut prendre des majorants/minorants un peu plus grossiers (et donc plus faciles à obtenir) voire même faire des études asymptotique pour en déduire que "à partir d'un certain rang on a ..." (ce qui souvent est plus simple) et que dans ce cas, tu obtient à la fin des constantes un peu moins bonnes que le 1/3 et le ln(4) ou bien uniquement une inégalité vraie "à partir d'un certain rang".
L'exo. est très calculatoire du fait qu'on veut obtenir à la fin des "vraies" constantes pas trop grandes et un inégalité valable pour tout n et pas seulement "à partir d'un certain rang".
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par Anonyme » 01 Déc 2010, 19:02
Benekire j'ai étudiée la suite :
J'ai trouve qu'elle est strictement croissante et pour n=3 u_n>1 ce qui conclu.
C'est de cette manière que tu as procédé ? car j'ai cru comprendre que tu allais utiliser l'inegalite moins précise (avec le 2n+1 au dénominateur).
Ben pour la 3a- tu as fait de la même manière ?
Et etes vous d'accord que c'est le cas n impair qui est trivial et non le cas n pair ?
J'ai trouve qu'elle est strictement croissante et pour n=3 u_n>1 ce qui conclu.
C'est de cette manière que tu as procédé ? car j'ai cru comprendre que tu allais utiliser l'inegalite moins précise (avec le 2n+1 au dénominateur).
Ben pour la 3a- tu as fait de la même manière ?
Et etes vous d'accord que c'est le cas n impair qui est trivial et non le cas n pair ?
par Ben314 » 01 Déc 2010, 19:15
Sinon, pour le 3)a), je fait le plus bètement du monde, par récurrence :
Amorce :
Hérédité : Si, pour un certain
, on a 
alors
}{n^2}\times\frac{4^{n-1}}{2\sqrt{n-1}}\ <\ {2n\choose n}=\frac{2n(2n-1)}{n^2}\times {2n-2\choose n-1}\ <\ \frac{2n(2n-1)}{n^2}\times4^{n-1}\)
et, pour conclure, il suffit de montrer que :
a)}{n^2}\times4^{n-1}\leq 4^n\ \Leftrightarrow\ 4n-2\leq 4n\ \)
: O.K.
b)}{n^2}\times\frac{4^{n-1}}{2\sqrt{n-1}}\ \ <br />\Leftrightarrow\ \ 2n\sqrt{n-1}\leq (2n-1)\sqrt{n}\ \ <br />\Leftrightarrow\ \ 4n^2(n-1)\leq (2n-1)^2n)
: O.K.
Amorce :
Hérédité : Si, pour un certain
a)
b)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par benekire2 » 01 Déc 2010, 20:04
Tu ruines tous mes espoirs pour la question 6 Ben ..
Comment je dois faire pour la question 6 , je ne vois plus du tout ?!
Merci!
Comment je dois faire pour la question 6 , je ne vois plus du tout ?!
Merci!
par Ben314 » 01 Déc 2010, 22:46
benekire2 a écrit:Tu ruines tous mes espoirs pour la question 6 Ben ..
Comment je dois faire pour la question 6 , je ne vois plus du tout ?!
Merci!
Effectivement, je pense qu'il y a une erreur (que je n'avais pas corrigée) et que dans le minorant de Rn, c'est 1/2.racine(2n) qu'il faut lire...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par benekire2 » 02 Déc 2010, 07:07
Ba alors je comprend carrement plus rien. Pour moi c est l exposant qui deconnais. Est-ce que tu peut reecrire cette question 6 en entier stp?
merci!!
merci!!
par Ben314 » 02 Déc 2010, 07:34
C'est bien dans l'exposant qu'il faut lire racine(2n) à la place de racine(n).benekire2 a écrit:Ba alors je comprend carrement plus rien. Pour moi c est l exposant qui deconnais. Est-ce que tu peut reecrire cette question 6 en entier stp?
merci!!
J'ai modifié...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par benekire2 » 02 Déc 2010, 09:26
Ok merci! et pour la toute derniere minoration qui acheve la demo comment je peut faire?
Merci encore !
Merci encore !
par Sylviel » 02 Déc 2010, 13:59
A vue de nez de ton inégalité ^{\frac{n}{3ln(n)}+\frac{\sqrt{2n}}{2}}2\sqrt{ n})
(c'est bien de celle là dont tu parles ?), je pense qu'une étude de fonction bourrine (éventuellement numérique) devrait faire l'affaire, non ?
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
par benekire2 » 02 Déc 2010, 21:45
Euh, pour l'étude de fonctions , c'est trop brutal pour moi, wolfram me donne une dérivée longue comme le bras , quelqu'un a réussi a la faire ? Ou alors y a plus rapide ? :triste:
par Ben314 » 02 Déc 2010, 23:29
De l'inégalité }} {2\sqrt{n}(2n)^{( \frac{1}{2}\sqrt{2n} )}}\ \leq\ (2n)^{(\pi(2n)-\pi(n) )})
on déduit que -\pi(n)\ \geq\ \frac{n}{3\ln(n)} K_n)
où
}{n}\times \frac{1}{\ln(2n)} \left( \frac{n}{3}\ln(4) - \ln\left(2\sqrt{n}\right) - \frac{1}{2}\sqrt{2n}\ln(2n) \right)<br />\ =\ <br />\frac{\ln(n)}{\ln(2n)} \left( \ln(4) - \frac{3\ln\left(2\sqrt{n}\right)}{n} - \frac{3 \ln(2n)}{\sqrt{2n}} \right))
}{\ln(2n)}\right) \left( \ln(4) - \frac{3\ln(2)}{n}<br />- \frac{3\ln(n)}{2n} - \frac{3 \ln(2)}{\sqrt{2n}} - \frac{3 \ln(n)}{\sqrt{2n}} \right))
Les fonctions}{x})
et }{\sqrt{x}})
ont pour dérivées respectives }{x^2}e)
et }{2x\sqrt{x}}e^2)
donc la suite _{n\geq 8})
est croissante et elle tend vers >1)
donc elle est 
à partir d'un certain rang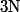 
facilement évaluable vu qu'il suffit que 
Mais là où ça déconne, c'est que
semble quand même trés grand...
Il doit y avoir (encore) une faute de frappe quelque part : je regarde demain.
Les fonctions
Mais là où ça déconne, c'est que
Il doit y avoir (encore) une faute de frappe quelque part : je regarde demain.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par benekire2 » 03 Déc 2010, 09:40
Ba il ne semble pas y avoir d erreur de calcul a premiere vue... Merci. Beaucoup pour la methode! !!
par ffpower » 03 Déc 2010, 11:46
Une question : pour 3) b) et c), vous arrivez à vous en sortir sans utiliser la formule de la valuation p-adique de n! ( et donc de C(2n,n) ) ?
( D'ailleurs je viens juste de remarquer, mais b) n'est rien de plus qu'un cas particulier de c) )
( D'ailleurs je viens juste de remarquer, mais b) n'est rien de plus qu'un cas particulier de c) )
par benekire2 » 03 Déc 2010, 11:57
Perso j ai fait comme toi mais ca doit pas etre durde faire sans. ..
par Euler07 » 03 Déc 2010, 13:26
benekire2 a écrit:Bonsoir ,
Un petit "défi" même si je suis pas sûr de ce que ça vaut :
-On admet que pour tout entier n>1 il existe un nombre premier p tel que n<p<2n
-On admet ou démontrera que p est un nombre premier si et seulement si p divise (p-1)!+1
Montrer que le n-ième nombre premier est :
Avecla partie entière
Amusez vous bien :lol3:
Une "énorme" indic : Testez pour n=3
J'espère ne jamais rencontrer une formule pareil de ma vie :dodo:
59 messages
- Page 2 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :