Une formule pour les nombres premiers

[benekire2]

Bonsoir ,

Un petit "défi" même si je suis pas sûr de ce que ça vaut :

-On admet que pour tout entier n>1 il existe un nombre premier p tel que n<p<2n
-On admet ou démontrera que p est un nombre premier si et seulement si p divise (p-1)!+1

Montrer que le n-ième nombre premier est :



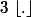
Avec la partie entière

Amusez vous bien :lol3:

Une "énorme" indic : Testez pour n=3

[benekire2]

C'est pas intéressant, trop inutile , trop barbare ? :cry:

[Anonyme]

C'est pas intéressant, trop inutile , trop barbare ?

Si si ça m’intéresse mais vu la forme barbare de la formule je me sis que ça va me prendre beaucoup de temps ( pour comprendre déjà ce que fait la formule :p) ) et la je dois réviser pour mon ds. Pour moi ça sera pour demain ou après demain (normalement). J'aimerai aussi démontrer les lemmes surtout le 1er avant d'attaquer la formule si c'est accessible en tout cas (mes connaissances en arithmetiques ne dépassent presque pas le programme de TS spe)

[darkpseudo]

Oo démontrer le premier lemme ... bonne chance , c'est un postulat vraaaiiiment corser !
Sinon pour ta formule elle est connu mais complètement inutile :)

[benekire2]

Le premier lemme c'est le postulat de Bertrand, j'ai jamais trop regardé la preuve. Pour le deuxième , c'est pas dur, travaille dans Z/pZ et regroupes les éléments avec leurs inverses.

Sinon, la formule et totalement inutile et une fois comprise ( une fois ça fait la démonstration en découle) on sent qu'elle est en carton ... mais bien montée quand même !!

[Sylviel]

Pour le postulat de Bertrand (démontré depuis un moment) on peux trouver la preuve dans proofs from THE BOOK, un bouquin qui devrait plaire à tous les fana de maths. Elle n'utilise que des outils élémentaires, mais elle est loin d'être évidente... Et certainement pas trouvable "comme ça". Si ça vous intéressent vraiment de la trouver par vous même je peux découper la preuve en questions plus simples... Mais comme c'est fastidieux je ne le fais que si quelqu'un est vraiment motivé ;-)

[benekire2]

Ba , j'ai trouvé la preuve de Erdos, je vais en faire un découpage si tu veut Sylviel ça t'évitera de le faire.

[Anonyme]

Je veux bien un découpage :D

[Ben314]

D'aprés Ellison :
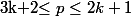
1) Montrer que si avec premier alors divise le coefficient binomial .
En déduire que on a :
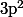
a) alors ne divise pas
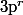
c) Si premier et divise alors .
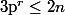
d) Si premier et tel que

[benekire2]

[quote="Ben314"]D'aprés Ellison :
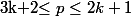
1) Montrer que si avec premier alors divise le coefficient binomial .
En déduire que [TEX]3$\prod_{pm+1 (qu'on appelle P) et le micro lemme de cette même question montre que P|C(2m+1,m+1) <2^m ce qui apporte le résultat.[/COLOR]

Perso tes sous questions sont pas triviales :zen: J'en suis à la 5 mais pour pas trop me prendre la tête j'ai pris les valuations p adiques dans la question 3.

[benekire2]

d) Si premier et tel que alors ne divise pas

Au passage , c'est faux, en revanche pour p entre 2/3 n et n là ça fonctionne , enfin amha , simple erreur de frappe je présume.

[Ben314]

Au passage , c'est faux, en revanche pour p entre 2/3 n et n là ça fonctionne , enfin amha , simple erreur de frappe je présume.

Effectivement : je modifie...
Sinon, concernant le 1), ben je fait comme l'énoncé le suggère, c'est à dire par récurrence (forte) ; pour montrer que le résultat est vrai pour n, j'utilise le fait que :
-Il était vrai pour n-1 si n est pair -> trivial.
-Il était vrai pour k=(n-1)/2 si n est impair et il suffit de majorer le pour conclure.

Donc, en résumé, je fait... comme toi.

[ffpower]

En fait, c'est vrai puisque l'ensemble vide vérifie n'importe quoi :)
Mais ya probablement une coquille ouais. Autres commentaires :


-Je suis pas sur d'avoir vu ou est-ce que 2) sert..( Bon j'ai pas regarder en détail aussi )

-La minoration de 3)a) n'est pas évidente. Normalement minorer en 4^n/n suffit ( je pense avoir une idée pour obtenir cette minoration plus fine, mais à moins qu'il y ait plus simple que ce que je pense il vaut mieux s'en passer ). Et au passage cette question me semblerait plutot devoir être posée au début vu qu'on utilise la majoration dans la question 1.

-La question 5 ne semble pas utile pour démontrer le postulat de Bertrand. Elle semble là juste histoire
d'avoir une majoration de pi(2n)-pi(n) ( on cherche une minoration, alors pourquoi pas une majoration au passage..Par contre je l'aurais perso mise plutôt dans l'exercice )

-A la 6, l'encadrement de Rn ne semble pas utiliser le fait que n>98. Cette condition ne devrait pas plutot se situer après, pour le "En déduire que" ? ( j'ai pas vérifié ce passage )

-Pour ceux qui veulent juste démontrer le postulat de Bertrand, sans aucunes estimations explicites devraient, en plus d'oublier la 5), supposer qu'il n'y a pas de nombres premiers entre n et 2n, comme ça Rn=1 et ça simplifie un peu les calculs..

[benekire2]

En fait, c'est vrai puisque l'ensemble vide vérifie n'importe quoi
Mais ya probablement une coquille ouais. Autres commentaires :

-Je suis pas sur d'avoir vu ou est-ce que 2) sert..( Bon j'ai pas regarder en détail aussi )
-La minoration de 3)a) n'est pas évidente. Normalement minorer en 4^n/n suffit ( je pense avoir une idée pour obtenir cette minoration plus fine, mais à moins qu'il y ait plus simple que ce que je pense il vaut mieux s'en passer ). Et au passage cette question me semblerait plutot devoir être posée au début vu qu'on utilise la majoration dans la question 1.
-La question 5 ne semble pas utile pour démontrer le postulat de Bertrand. Elle semble là juste histoire
d'avoir une majoration de pi(2n)-pi(n) ( on cherche une minoration, alors pourquoi pas une majoration au passage..Par contre je l'aurais perso mise plutôt dans l'exercice )
-A la 6, l'encadrement de Rn ne semble pas utiliser le fait que n>98. Cette condition ne devrait pas plutot se situer après, pour le "En déduire que" ? ( j'ai pas vérifié ce passage )

Salut , concernant la 2 , et ba j'en suis a la 5 ( pas commencée) et elle m'apas encore servis.

Sinon, pour la minoration 3a ba d'habitude je minore par 4^n/(2n+1) et pour l'affiner je bourrine, rien de plus.

PS. Enfin, jusqu'à présent ce problème est pas évident , merci Ben :we:

[ffpower]

Tu bourrines comment? ( moi j'ai utilisé la formule exprimant la somme des C(2n,k)² )

[benekire2]

Tu bourrines comment? ( moi j'ai utilisé la formule exprimant la somme des C(2n,k)² )

Je te retourne la question : Je veut bien voir comment tu fais également :we:

Perso : J'étudie les variations de C(2n,n) * (racine(n)/4^n)

[ffpower]

Non bah ma méthode marche pas en fait :happy2:

[Ben314]

Concernant la formulation, je me suis fait zéro chier : j'ai repris presque exactement l'exo du Ellison.
Bien entendu, si on ne veut "que" Bertrand ou si on s'en fout d'avoir des constantes "explicites" dans l'encadrement final, on peut aller nettement plus vite en majorant/minorant "à la va vite".

Je pense que l'objectif de l'exo était de montrer que, en étant très soigneux dans les encadrements on peut, avec une seule idée (celle de considérer le coeff. binomial (2n n)), avoir des constantes explicites pas monstrueusement grandes/petites.

[benekire2]

Bon de retour après mangé , je viens de faire la 5 :

Le produit des p pour n<p<2n est inférieur a 4^n et puis en passant au logarithme ce bazar on a que la somme des ln(p) est inférieur à nln(4) ce qui nous amène a minorer cette somme de logarithmes par (pi(2n)-pi(n))ln(n) qui fournit le résultat.

Je vais voir la 6 dans pas trop longtemps. Et sinon, plusieurs questions déjà :

- Les ln(n)/n me rappelle le théorème des nombres premiers ( dont j'ai pas encore lu la preuve mais ça peut attendre :zen: ) on pourrait pas le "déduire" de ça ou alors c'est vraiment autre chose ? ( Je n'y ai pas trop réfléchi, il se pourrait donc que ma question soit totalement stupide)

- Ben, quand tu dit "majorer à la va vite" de quoi tu veut parler ?? J'ai essayé mais je dois encore montrer que est faux pour n suffisamment grand :mur:

Il semble que dans ce topic le postulat de bertrand soit plus intéressant que la formule pour les nombres premiers :ptdr:

[benekire2]

Au passage Ben , comment fait tu la question 3a ?

Sinon, j'ai fais le début de la question 6 :

D'aprés Ellison :
6) Montrer que, si alors

Sauf que j'obtiens [TEX]3$\frac{4^{(\frac{n}{3})}} {2\sqrt{n}(2n)^{(\frac{1}{2}\sqrt{2n})}}\ 98 et par récurrence c'est plus que la misère !!