Une fonction pour 2014
2 messages
- Page 1 sur 1
par Ben314 » 11 Nov 2013, 03:20
Salut,
Si + 2 f(n) = 3n + \lambda\)
(où 
est une constante entière), on montre facilement que, si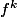 
désigne 
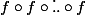(k fois) alors, pour tout 
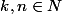on a:
=\frac{1-(-3)^k}{4}f(n)+\frac{(-3)^k+3}{4}n +\lambda\frac{(-3)^k-1+4k}{16})
Or cette quantités est un entier naturel donc elle est positive ce qui implique que :
\ \leq\ \frac{(-3)^k+3}{(-3)^k-1}n +\lambda\Big(\frac{1}{4}+\frac{k}{(-3)^k-1}\Big)\)
pour tout 
pair d'où (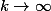
) \leq n+\frac{\lambda}{4})
\ \geq\ \frac{(-3)^k+3}{(-3)^k-1}n +\lambda\Big(\frac{1}{4}+\frac{k}{(-3)^k-1}\Big)\)
pour tout impair d'où (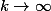) \geq n+\frac{\lambda}{4})
En particulier, il n'y a pas de solutions si n'est pas multiple de 4.
P.S. Tu sait aussi "tripoter" les trois autres coeff (le 1 devant le fof(n), le 2 devant le f(n) et le 3 devant le n) : c'est... un peu plus délicat...
Si
Or cette quantités est un entier naturel donc elle est positive ce qui implique que :
En particulier, il n'y a pas de solutions si
P.S. Tu sait aussi "tripoter" les trois autres coeff (le 1 devant le fof(n), le 2 devant le f(n) et le 3 devant le n) : c'est... un peu plus délicat...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :