Une équation + une inégalité géométrique
Olympiades mathématiques, énigmes et défis
-
laya
- Membre Relatif
- Messages: 128
- Enregistré le: 06 Déc 2010, 20:12
-
 par laya » 27 Déc 2010, 18:25
par laya » 27 Déc 2010, 18:25
Bonjour,
Je suis nouveau sur ce forum, je précise que je suis en école d'ing, j'ai participé dans le temps aux olympiades et j'aime toujours autant ces compétitions. Voilà pourquoi je propose deux problèmes de difficulté croissante :
1. Une petite équation (niveau Première et +), de moi (d'où la relative mocheté :lol3: ):
Soient a et b deux réels. Trouver tous les triplets de réels strictement positifs (x,y,z) vérifiant :
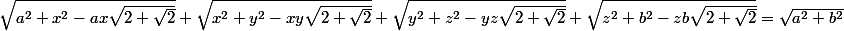
2.Une inégalité géométrique
P est un point intérieur à un triangle ABC. A', B' et C' sont respectivement ses projetés orthogonaux sur (BC), (AC) et (AB).
Montrer que :
)
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 27 Déc 2010, 19:56
par Zweig » 27 Déc 2010, 19:56
Salut,
Pour ton équation, je passerai bien par du Al-Kashi (et donc une interprétation géométrique de la relation, le membre de droite me faisant penser à Pythagore) dès que j'aurai trouvé à quel angle correspond
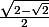
....
-
Anonyme
 par Anonyme » 27 Déc 2010, 20:16
par Anonyme » 27 Déc 2010, 20:16
C'est 3pi/8
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 27 Déc 2010, 20:21
par Zweig » 27 Déc 2010, 20:21
Oui, je l'ai trouvé entre temps :zen:
-
Anonyme
 par Anonyme » 27 Déc 2010, 20:23
par Anonyme » 27 Déc 2010, 20:23
Zweig a écrit:Oui, je l'ai trouvé entre temps :zen:
J'imagine, je postais pour ceux qui ont la flemme :lol3: Sinon ca fais une belle figure .
-
laya
- Membre Relatif
- Messages: 128
- Enregistré le: 06 Déc 2010, 20:12
-
 par laya » 27 Déc 2010, 20:24
par laya » 27 Déc 2010, 20:24
Qmath a écrit:C'est 3pi/8
Pourquoi 3pi/8 ?
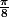
suffit :lol3:
-
Anonyme
 par Anonyme » 27 Déc 2010, 20:35
par Anonyme » 27 Déc 2010, 20:35
Avec pi/8 je vois pas trop comment faire
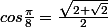
et pas
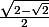
.
Je me precipite probablement mais je pense qu'il n'existe pas un tel triplet (x,y,z) étant donne que le segment est le plus court chemin reliant 2 points.
-
Malo
- Membre Naturel
- Messages: 33
- Enregistré le: 29 Oct 2010, 16:50
-
 par Malo » 27 Déc 2010, 20:40
par Malo » 27 Déc 2010, 20:40
Et entre guillemets tu es toujours aussi analphabète. L'orthographe, c'est fait pour les chiens ?
-
Anonyme
 par Anonyme » 27 Déc 2010, 20:48
par Anonyme » 27 Déc 2010, 20:48
Tu peux changer de pseudo/comptes autant que tu veux on te reconnaitra toujours :lol3: toujours aussi désagréable :ptdr:
Merci pour la confirmation .
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 27 Déc 2010, 20:51
par Zweig » 27 Déc 2010, 20:51
Titux ? :marteau:
-
Anonyme
 par Anonyme » 27 Déc 2010, 20:53
par Anonyme » 27 Déc 2010, 20:53
Bingo :ptdr: Aussi connu sous le pseudo Mathx qui comme par hasard a arrêté de poster quand Malo s'est inscrit :ptdr:
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 27 Déc 2010, 21:08
par Zweig » 27 Déc 2010, 21:08
Message supprimé ^^ Quel gland ...
-
Anonyme
 par Anonyme » 27 Déc 2010, 21:22
par Anonyme » 27 Déc 2010, 21:22
No comment ^^
Au fait Zweig as tu trouvé le même résultat que moi a savoir qu'il n'existe pas un tel triplet ?
-
laya
- Membre Relatif
- Messages: 128
- Enregistré le: 06 Déc 2010, 20:12
-
 par laya » 27 Déc 2010, 23:55
par laya » 27 Déc 2010, 23:55
Désolé les gars, j'aurais bien dû mettre
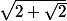
, j'ai corrigé dans le message d'origine. Quoiqu'il en soit, vous êtes évidemment sur la bonne piste.
-
laya
- Membre Relatif
- Messages: 128
- Enregistré le: 06 Déc 2010, 20:12
-
 par laya » 29 Déc 2010, 13:42
par laya » 29 Déc 2010, 13:42
Alors, personne ? Surtout pour l'inégalité géométrique qui a une petite histoire que je raconterai une fois que vous aurez essayé. Je peux donner des indications puisque je connais la solution.
-
Anonyme
 par Anonyme » 29 Déc 2010, 14:23
par Anonyme » 29 Déc 2010, 14:23
Pour la 1ere je pense pouvoir m'en sortir mais les calculs doivent être horribles. Déjà graphiquement il y a évidemment une solution après pour calculer x, y, z en fonction de a et b je pense qu'utiliser Al kashi est tres moche et qu'il est plus judicieux d'utiliser la loi de proportion relative a la bissectrice mais j'ai pas le courage de rentrer dans tous ces calculs :marteau: Lidée est-elle correcte au moins ?
Pour la 2/ j'ai pas encore regarde lénoncé mais déjà la 1/ n'est pas facile pour un 1S.

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 29 Déc 2010, 14:33
par Olympus » 29 Déc 2010, 14:33
Dommage que l'inégalité est géométrique :cry: ... ( moi et la géométrie ... :zen: )
-
Anonyme
 par Anonyme » 29 Déc 2010, 15:05
par Anonyme » 29 Déc 2010, 15:05
Je suis arrivé a
)
avec
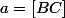
,
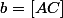
et
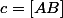
.
Maintenant je ne pense plus qu'elle tienne de la géométrie..
-
Anonyme
 par Anonyme » 29 Déc 2010, 15:09
par Anonyme » 29 Déc 2010, 15:09
Je suis arrivé a
)
avec
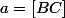
,
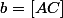
et
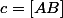
.
Maintenant je ne pense plus qu'elle tienne de la géométrie..
Edit: non ça reste une inégalité géométrique ...
-
laya
- Membre Relatif
- Messages: 128
- Enregistré le: 06 Déc 2010, 20:12
-
 par laya » 29 Déc 2010, 15:57
par laya » 29 Déc 2010, 15:57
Qmath a écrit:Je suis arrivé a
)
avec
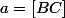
,
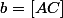
et
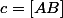
.
Maintenant je ne pense plus qu'elle tienne de la géométrie..
Edit: non ça reste une inégalité géométrique ...
Oui mais le passage de cette inégalité sur les aires (celle que tu as trouvée) à une inégalité sur les longueurs (celle demandée) ne va pas être aisé. Dans le cas limite où ABC est un triangle équilatéral, les deux inégalités sont équivalentes et sont en fait des égalités.
La preuve de cette inégalité a été fournie en 1937 (elle est donc assez récente).
Voici une indication :
Montrer d'abord que :
}{sin(A)}PB'+\frac{sin(B)}{sin(A)}PC')
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
