Une équation différentielle

[Dacu]

Bonjour à tous,

Résoudre l'équation , où avec .

Cordialement,

Dacu

[zygomatique]

salut

en excluant les cas particuliers (genre b = 1) ...

donc f est C-infinie ...

af'(x + u) - (b - 1)f(x) = 0 => af"(x + u) - (b - 1)f'(x) = 0 (*)

en posant x = x + u : (*) <=> af"(x) - (b - 1) f'(x + u) = 0

donc

a(b - 1)f'(x + u) - (b - 1)(b - 1)f(x) = 0
aaf"(x) - a(b - 1)f'(x + u) = 0

en ajoutant membre à membre qui est un classique ...

[Ben314]

Salut,

af'(x + u) - (b - 1)f(x) = 0 => af"(x + u) - (b - 1)f'(x) = 0 (*)

en posant X = x + u : (*) <=> af"(X) - (b - 1) f'(X-u) = 0

Et surement pas f'(X+u) vu que l'inverse de la translation x->x+u ça risque pas d'être elle même.
Tout ce que dit l'équation, c'est une "relation de périodicité" et il y a une énorme multitude de solution : on prend quasiment n'importe quelle fonction "de base" C^infini sur un certain intervalle de longueur u et la relation donnée explique uniquement comment prolonger de façon unique la fonction à R tout entier. Et comme la relation ne dit rien d'autre que ça (i.e. comment prolonger), je vois vraiment pas ce qu'on peut écrire d'un tant soit peu pertinent concernant cette énorme infinité de solutions.
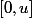
Dans ce type de contexte (formule "de périodicité") la seule question qu'on peut se poser, c'est de regarder quelle sont les condition que doit vérifier la fonction "de base" au bord de l'intervalle (de largeur u) pour que ça se recolle proprement lors des "recopies", sauf que là, c'est totalement trivial : si par exemple on part de l'intervalle , pour que tout se passe bien, il faut évidement que pour tout 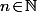on ait .

Bref, ça a à eu prés autant d'intérêt comme énoncé que "Résoudre l'équation fonctionnelle f(x+1)=f(x) pour tout x"