Une contribution d'Euler
Olympiades mathématiques, énigmes et défis
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 07 Mar 2008, 18:09
par Zweig » 07 Mar 2008, 18:09
Ce problème a été inventé par Euler (que je ne présente plus :ptdr:) qui ne l'a jamais publié. Ce sont les organisateurs des olympiades russes qui ont retrouvé ce problème dans les notes d'Euler et l'ont proposé à l'olympiade russe, où personne n'a pu donné une solution :marteau:

... C'est donc un problème ultra-difficile, donc je vous laisse chercher et je vous donnerais, si vous séchez, la brillante solution donnée par un membre de l'équipe allemande des OIM, Eric Müller.
Voici le problème :
Montrer que si
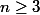
, alors

peut être représenté sous la forme
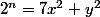
, avec

et

impairs.
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 07 Mar 2008, 18:26
par ffpower » 07 Mar 2008, 18:26
ouais,on sent que c est le genre de truc pas facile.je prefere les equations fonctionelles lol
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 07 Mar 2008, 19:28
par _-Gaara-_ » 07 Mar 2008, 19:28
Salut Zweig,
Zweig a écrit:vous séchez, la brillante solution donnée par un membre de l'équipe allemande des OIM, Eric Müller.
Bah ouais, Deutch ist gut après tout ^^
Dis pour la démonstration, c'est astucieux ou il faut connaître un théorème précis ? :help:
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 07 Mar 2008, 19:42
par Zweig » 07 Mar 2008, 19:42
C'est de l'astuce principalement.
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 07 Mar 2008, 20:16
par _-Gaara-_ » 07 Mar 2008, 20:16
bon je me lance mais je ne sais même pas si c'est bon.. Bref ^^
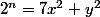
eq
} = 7 e^{2\ln(x)} + e^{2\ln(y)})
eq
 = \ln(7) + 2\ln(x) + 2\ln(y))
eq
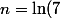}{\ln(2)} + \fr{2\ln(x)}{\ln(2)} + \fr{2\ln(y)}{\ln(2)})
eq
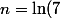}{\ln(2)} + 2\log_2(xy))
x impair et y impair donc
x=2k+1
y= 2m+1
eq
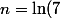}{\ln(2)} + 2\log_2(4km+2k+2m+1))
donc
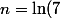}{\ln(2)} + \log_2((4km+2k+2m+1)^2))
tout çà pour çà quoi.. Je ne sais pas s'il existe un truc pour pouvoir torcher çà direct..
Maitenant reste à démontrer que tout nombre n supérieur ou égal à 3 peut s'écrire sous cette forme et c'est fini.... :briques:
Tu as une indication Zweig ?? :we:
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 07 Mar 2008, 20:25
par Zweig » 07 Mar 2008, 20:25
Les mots maîtres ici sont "récurrence" et "tableau" ... Pourquoi "tableau" ? Parce que la réponse se trouve dans la tableau que vous aurez dressé via la récurrence sur les premières valeurs de

... Essayez de trouver une relation pour passer de la paire
)
d'une colonne à la paire
)
de la colonne suivante !
n |3|4| ....
-------------
x |..|..| ....
-------------
y |..|..|....
-------------
Conjecturez cette relation, puis démontrez-la !
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 07 Mar 2008, 20:30
par _-Gaara-_ » 07 Mar 2008, 20:30
Zweig a écrit:
n |1|2| ....
-------------
x |..|..| ....
-------------
y |..|..|....
-------------
Il ne faut pas commencer par n = 3 normalement ? :hein:
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 07 Mar 2008, 20:32
par Zweig » 07 Mar 2008, 20:32
Si si bien sûr, j'ai tapé trop vite, comme d'hab, je ne me relis pas :dodo:
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 07 Mar 2008, 20:49
par _-Gaara-_ » 07 Mar 2008, 20:49
n |3|4|5|6|7|
-------------
x |1|1|1|..
-------------
y |1|3|5|..
-------------
je ne vois pas la relation oO
Mais dis, ce que j'ai fait c'est n'importe quoi ? oO :cry:
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 07 Mar 2008, 20:55
par _-Gaara-_ » 07 Mar 2008, 20:55
C'est pas par hasard les termes impairs de la suite de fibonacci ? xD
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 07 Mar 2008, 21:05
par ThSQ » 07 Mar 2008, 21:05
Je l'ai vu l'an dernier. C'est atrocement astucieux.
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 07 Mar 2008, 21:21
par _-Gaara-_ » 07 Mar 2008, 21:21
ThSQ a écrit:Je l'ai vu l'an dernier. C'est atrocement astucieux.
lol si tu le dis c'est que c'est hyper dur :doh:
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 07 Mar 2008, 21:29
par Zweig » 07 Mar 2008, 21:29
Non Gaara, pas de Fibbonaci dans l'air ... En fait, y'a besoin de se servir d'aucun théorème déjà connu. Dès lors que tu as trouvé la (enfin les) relations liant chaque couple d'une colonne à la suivante, alors t'as déjà fait le plus gros boulot.
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 07 Mai 2008, 00:44
par Joker62 » 07 Mai 2008, 00:44
étrangemment, moi qui n'aime pas du tout ces espèces de problèmes, j'avoue craqué totalement pour celui-ci :)
Merci ;)
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 07 Mai 2008, 09:17
par lapras » 07 Mai 2008, 09:17
Tout simplement incroyable.
La relation entre les x et les y était difficile à remarquer. J'aime bien le coup du facteur 7 ajouté car on a un 7 dans l'équation lol.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités