Trouvons l'erreur ^^
Olympiades mathématiques, énigmes et défis
-
samah
- Membre Relatif
- Messages: 257
- Enregistré le: 01 Juil 2008, 22:49
-
 par samah » 02 Juil 2008, 23:04
par samah » 02 Juil 2008, 23:04
Salut
Trouvez l'erreur
-1=(-1)^1=(-1)^(2*1/2)=((-1)^2)^1/2=(1)^1/2=1
conclusion: -1=1
:doh:
-
samah
- Membre Relatif
- Messages: 257
- Enregistré le: 01 Juil 2008, 22:49
-
 par samah » 02 Juil 2008, 23:05
par samah » 02 Juil 2008, 23:05
Bonne chance ^.^

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 02 Juil 2008, 23:13
par raito123 » 02 Juil 2008, 23:13
Déja vu des dizaines de fois sur le forum ^^
Les multiples ne doivent pas être utilisés sans nécessité
-
samah
- Membre Relatif
- Messages: 257
- Enregistré le: 01 Juil 2008, 22:49
-
 par samah » 03 Juil 2008, 01:18
par samah » 03 Juil 2008, 01:18
raito123 a écrit:Déja vu des dizaines de fois sur le forum ^^
j savé po .. :p
-
john32
- Membre Relatif
- Messages: 239
- Enregistré le: 08 Juil 2008, 10:34
-
 par john32 » 24 Juil 2008, 14:44
par john32 » 24 Juil 2008, 14:44
C'est une histoire de priorité mais je trouve pas l'erreur ! :doh:
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 24 Juil 2008, 15:09
par _-Gaara-_ » 24 Juil 2008, 15:09
Salut,
a^x = e^(x ln(a))
on voit bien que la fonction puissance est définie pour a dans ]0; + infini [
ce qui n'est pas le cas ici xD
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 24 Juil 2008, 15:13
par Clembou » 24 Juil 2008, 15:13
samah a écrit:Salut
Trouvez l'erreur
-1=(-1)^1=(-1)^(2*1/2)=((-1)^2)^1/2=(1)^1/2=1
conclusion: -1=1
:doh:
Problème au passage de :
^{2*1/2} = ((-1)^2)^{1/2})

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 24 Juil 2008, 15:14
par raito123 » 24 Juil 2008, 15:14
Je suis pas dac avec toi Gaara !!(((
Les multiples ne doivent pas être utilisés sans nécessité
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 24 Juil 2008, 15:14
par _-Gaara-_ » 24 Juil 2008, 15:14
Ahhhh !! je viens de tomber sur un truc philosophique :
i² = e^(2 ln(i) )
Que vaut ln (i) ????????
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 24 Juil 2008, 15:25
par _-Gaara-_ » 24 Juil 2008, 15:25
raito123 a écrit:Je suis pas dac avec toi Gaara !!(((
Pourquoi ? j'ai fait quoi SNIF XD
Merci Clembou ^^ Trop joli le résultat xD ^^

-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 24 Juil 2008, 15:27
par Clembou » 24 Juil 2008, 15:27
_-Gaara-_ a écrit:Pourquoi ? j'ai fait quoi SNIF XD
Merci Clembou ^^
Parce que il faut trouver une autre définition de la puissance pour les nombres négatifs :we: .
C'est pas parce que
^n)
ne peut pas s'écrire sous la forme d'exponentielle que cela n'existe pas :id:
EDIT : En fait je pense que MAPLE fait cela pour avoir
)
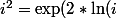))
 = 2*\ln(i))
 = \ln(i))
et
 = i\pi)
(je sais pas d'où viens cette formule par contre)
et donc :
 = \frac{1}{2}i\pi)
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 24 Juil 2008, 15:41
par _-Gaara-_ » 24 Juil 2008, 15:41
Génial Clembou
encore merci ^^ et je viens de me rendre compte qu'en effet, pour a négatif on a : a^x = (ln ( e^a))^x ;)=
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 24 Juil 2008, 15:53
par Clembou » 24 Juil 2008, 15:53
Je rebondis sur mon précédent post en étant étonné. Pourquoi ?
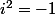
et le logarithme est quand même défini :doh:
 = i\pi)
Certes, le résultat est sous la forme d'un complexe. Cela voudrait dire que :
=y)
Impressionnant comme résultat :id:
-
Imod
- Habitué(e)
- Messages: 6483
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 24 Juil 2008, 16:52
par Imod » 24 Juil 2008, 16:52
Tu peux très bien définir
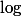
sur
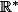
mais il ne faut pas oublier qu'il n'existe pas de détermination du logarithme sur
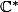
.
Imod
-
le_fabien
- Membre Complexe
- Messages: 2737
- Enregistré le: 05 Oct 2007, 10:00
-
 par le_fabien » 24 Juil 2008, 17:19
par le_fabien » 24 Juil 2008, 17:19
samah a écrit:Salut
Trouvez l'erreur
-1=(-1)^1=(-1)^(2*1/2)=((-1)^2)^1/2=(1)^1/2=1
conclusion: -1=1
:doh:
Bonsoir,
tu prétends donc que
^2}=1)
donc en général que
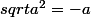
...
Bizarre cela me parait pas très rigoureux.. :hum:
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 24 Juil 2008, 17:29
par Flodelarab » 24 Juil 2008, 17:29
LEFAB11 a écrit:Bonsoir,
tu prétends donc que
^2}=1)
donc en général que
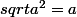
...
Bizarre cela me parait pas très rigoureux.. :hum:
Pardon mais je ne comprends absolument pas le rapport. D'autant plus que la deuxième partie de ta phrase n'est pas isomorphe avec la première partie. D'abord tu parle d'un cas particulier de
^2}=-a)
car a est négatif et après
^2}=a)
(ou a est vraisemblablement positif mais peut importe)
Ta généralisation est différente de ton cas particulier
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 24 Juil 2008, 17:32
par Flodelarab » 24 Juil 2008, 17:32
LEFAB11 a écrit:Bonsoir,
tu prétends donc que
^2}=1)
donc en général que
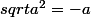
...
Bizarre cela me parait pas très rigoureux.. :hum:
ça ne te parait pas rigoureux et pourtant c'est vrai pour tout les a réels négatifs ...
Et ça n'a rien a voir avec la faute du premier post.
-
le_fabien
- Membre Complexe
- Messages: 2737
- Enregistré le: 05 Oct 2007, 10:00
-
 par le_fabien » 24 Juil 2008, 17:34
par le_fabien » 24 Juil 2008, 17:34
Je pense donc à la fonction

définie de IR dans IR+ alors il est normal que pour deux antécédents ( -1 et 1 ) on ait la même image 1.
Je pense que l'erreur vient de là.
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 24 Juil 2008, 17:38
par Flodelarab » 24 Juil 2008, 17:38
LEFAB11 a écrit:Je pense donc à la fonction

définie de IR dans IR+ alors il est normal que pour deux antécédents ( -1 et 1 ) on ait la même image 1.
Je pense que l'erreur vient de là.
L'erreur ne vient pas de là.
D'abord parce que personne n'a parlé de fonction et que tu raisonnes en terme de fonction.
Et puis aussi car personne n'a dit que
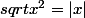
avait des images dans IR-
D'ailleurs, personne n'a parlé de la fonction racine carrée ....
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 8 invités
donc en général que
...
définie de IR dans IR+ alors il est normal que pour deux antécédents ( -1 et 1 ) on ait la même image 1.
